 PHYSICS FOR PROGRAMMERS
PHYSICS FOR PROGRAMMERS
Introduction
The following sections are intended as a concise but solid introductions to current scientific understanding
of the physical universe. We do not assume any prior knowledge of physics, but familiarity with
Multivectors as later described will be subsequently assumed.
Multivectors enable a clearer and cleaner picture than many standard treatments.
In this section we lay some basic groundwork in terms of units and scales, not all of which will make immediate sense to
the physics novice, who should skim over any terms, phrases, and equations he does not recognise.
The intent is to provide a programmers' perspective of what we might call the numerical playing field,
inpartcular the notion that every physical quantity can be measured in terms of a
a reference length unit such as the meter.
 Physical Units
Physical Units
Length
Because length, time, mass, energy, and temperature are all related,
we can measure all of them in various powers of the same unit. We will favour the
meter length unit m here since it is a particularly human-comprehendable measure.
Lightspeed c = 299 792 458 m s-1
» 228.16 m s-1 » 3×108 m s-1
provides 1 s = 299792458 m » 228.16 m,
where = denotes "unit equivalence",
in the sense that light travels that far in a second. We can write this as
1 s = c m but must be careful in that this c
is the m s-1 value without the units, for strictly speaking c m
has units m2 s-1 rather than s. We use = rather than =
to remind us that the units should be "stripped" and just the (S.I.) values used for variable symbols
like c and h;
and that the equivalence is predicated on the precise values used for these constants.
Our time unit becomes c-1 m, the time taken for light to travel one meter, and we can
effectively measure time in meters. Speed becomes unitless in the sense that we can measure all speeds as fractions of c
and can choose our units so that c=1. This is not the same as dimensionless. A
value is dimensionless if it has the same numeric value under every system of units.
The energy of a photon of wavelength l is given by
E=hcl-1
so we can measure energy in m-1 (the spacial frequency of a photon with the desired energy) with
1 J = (hc)-1 m-1 = 5.0327126 × 1024 m-1
where 1 J = 1 N m = 1 kg m2 s-2 is the S.I. Joule unit;
and 1 m = (hc)-1 J-1 = 5.0327126 × 1024 J-1 .
[ h = 6.626068 × 10-34 m2 kg s-1 is known as the Planck constant.
The Dirac-Planck Constant (aka. h-bar) h º (2p)-1 h
can be regarded as the fundamental quanta of angular momentum.
]
Via Einstein's E=Mc2 we have
1 kg = c2 J
= ch-1 m-1
so we can measure mass in energy units and so in inverse length units.
Temperature is merely a measure of energy and via E=kBT where kB is Boltzman's constant
we have 1 K = 1.38065×10-23 J so we
can measure temperature in energy as the energy per molecule of a reference ideal gas at the given temprature.
Thus we can measure mass, energy, temperature, frequency, and inverted length in a single S.I. unit such as m-1 or J or K [ Without reference to the universal gravtiational constant G = 6.6742×10-11 m3kg-1 =0×102147483647 m4 ]provided only that we have accurate values for c, h, and the Boltzmann temeperature-energy ratio kB. It is worth noting that kB » 8×5½×10-16h½c (within 0.014 %).
| S.I. Units Conversion Table based on c=2.99792×108 ms-1 ; h=6.62607×10-34 Js ; kB=1.38065×10-23 JK-1 |
| Unit | Length | Time | Mass | Energy | Temperature |
| m | 1 m | c-1 = 2-28.1594
=3.33564×10-9 s | ch-1 = 2138.377
=4.52444×1041 kg-1 | c-1h-1 = 282.058
=5.03412×1024 J-1 | c-1h-1kB = 26.11902
=6.95036×101 K-1 |
| s | c = 228.1594
=2.99792×108 m | 1 s | c2h-1 = 2166.536
=1.35639×1050 kg-1 | h-1 = 2110.217
=1.50919×1033 J-1 | h-1kB = 234.2784
=2.08366×1010 K-1 |
| kg | ch-1 = 2138.377
=4.52444×1041 m-1 | c2h-1 = 2166.536
=1.35639×1050 s-1 | 1 kg | c2 = 256.3188
=8.98755×1016 J | c2kB-1 = 2132.258
=6.50965×1039 K |
| J | c-1h-1 = 282.058
=5.03412×1024 m-1 | h-1 = 2110.217
=1.50919×1033 s-1 | c-2 = 2-56.3188
=1.11265×10-17 kg | 1 J | kB-1 = 275.939
=7.24296×1022 K |
| K | c-1h-1kB = 26.11902
=6.95036×101 m-1 | h-1kB = 234.2784
=2.08366×1010 s-1 | c-2kB = 2-132.258
=1.53618×10-40 kg | kB = 2-75.939
=1.38065×10-23 J | 1 K |
Charge
The charge of the electron is considered to be Qe- º e
= -1.60217646 × 10-19 C where C
denotes a Coulomb, the S.I. (Systematised Idiocy) unit of charge. This is defined as
one Amp Second A s where the Amp is defined as the current
producing a force of 2×10-7 Newtons per meter between two infinite wires one meter apart
, a disasterously misconcieved approach.
The Coulomb force law F = k q1q2 r-2
for two charges distance r apart suggests measuring charge in
f º
N½ m
= kg½ m3/2 s-1
= c-1 kg½ m½
= c-1 (ch-1 m-1)½ m½
= (ch)-½ m0
= (ch)-½
where ch is unit stripped, ie.
a dimensionless (unitless) measure.
The saner C.G.S. ("centimeter-gramme-second") system has the
equivalent Franklin or electro-static-unit
defined by 1 esu º 1 g½ cm3/2 s-1
= 10-3/2 kg½ 10-3 m3/2 s-1
= 10-9/2 f .
For the Lorentz-heaviside system we take k=(4p)½
but if we don't take this approach, k has to be given compensatory units and in S.I.
we have k = (4pe0)-1 = 10-7 c2
kg m C-2
and e0 =
(4p)-1 c-2 107
C2 kg-1 m-1 .
It turns out that 1 C = 10c esu
= 10-7/2 c f
where c is the m s-1 lightspeed value (with the units stripped)
so f = c-1 107/2 C = (ch)-½
and
1 C = 10-7/2 (ch-1)½ m0
yielding
Qe- = -1.60218×10-19 C = -4.8032×10-10 esu = -1.51891×10-14 f = -0.0340795 = -0.0340795 = -2-4.874952 = -(2pae--1)-½ = -(2p)-½ ae-½where dimensionless ae- » 137.036-1 » 2-7.0981 known as the fine structure constant provides a more traditional dimensionless measure of Qe-.
The Coulomb does not appear in the above S.I.
units conversion table because charge, having no units,
is effectively measured in m0;
though it is perhaps most natural to measure
charge in multiples of the electron charge Qe-,
or possibly of the downquark charge Qd = 3-1 Qe-
= 0.0113598 = 2-6.4599188 serving to remind us of natures strong indication that charge is an integer variable.
Benjamin Franklin's coin toss dictates that we consider
the electron charge Qe- [ often denoted e ] to be negative and the positron and proton charges (assumed both equal
to -Qe-) to be positive.
We are free to postulate an electron charge of -1 and interpret ae- as a measure of
nonunit e0=(4pae-)-1 , but physicists usually
favour taking either e0
= ½ae--1 (hc)-1Qe-2
or 4pe0
= 2pae--1 (hc)-1 Qe-2
to be unity
and so take Qe- to be either -(2ae-hc)½
or -(½p-1ae-hc)½
= -(ae-hc)½
, ie.
Qe- = -(2ae-)½ or
Qe- = -((2p)-1ae-)½
Regardless, permitivitties of other media
are usually considered as proportions of e0.
The Fine Structure Constant
As the most natural measure of the dimensionless electron charge, the fine structure constant
ae- = (2e0hc)-1Qe-2 = (2p)Qe-2
is arguably the primary empirically derived parameter of our universe. Its value cannot
currently be theorectically derived but must rather be directly or indirectly measured
experimentally and then "fed" into theories such as the Standard Model.
The best current estimates for ae-
are the
2006 QED-based value a2006=137.035999710(96)-1 and the 2002 CODATA value
a2002=137.03599911(46)-1 , with non-intersecting standard uncertainty ranges
[137.035999614, 137.035999806]
and
[137.035998650, 137.035999570] respectively .
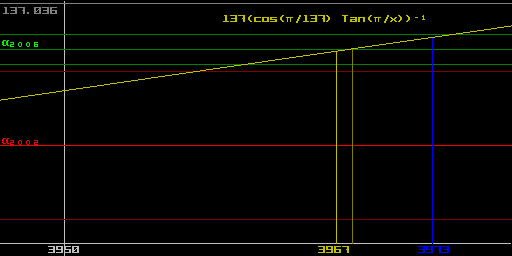
James Gilson suggests
ae-=137-1 cos(137-1p) Tan(n-1p)
where integer n=3973=137×29 and Tan(x) º x-1 tan(x) is the
cardinal tangent function.
This lies within the a2006 uncertainty range but the n giving closest
approximation to a2006 is
n=3968=(25-1)×27
with 137-1 cos(137-1p) Tan(3968-1p) = 137.0359997146-1 .
However
n=3967 is almost as good with 137-1 cos(137-1p) Tan(3967-1p) = 137.035999700237-1
and 3967 is the (137×4)th prime (if 2 is considered the 0th prime)
, which is either a remarkable coincidence
or a strong indication that Gilson is on the right track.
|
|
Setting HN º åk=1N (-1)½k(k-1) k!
we observe that H5 = 1!-2!-3!+4!+5!=137 and
letting Pk denote the kth prime we thus have the equivalent conjectures
ae- = HN -1 cos(HN -1 p) Tan(P(N-1)HN -1 p)
and
ae- = HN -1 cos(HN -1 p) Tan(P4HN -1 p)
for N=5.
Composite Units
The Newton unit of force 1 N = 1 kg m s-2
= ch-1 m-1 m (c m)-2
= (ch)-1 m-2 while the Pascal unit of pressure is 1 Pa
= 1 Nm-2
= (ch)-1 m-4 .
Density in kg m-3 = ch-1 m-4 thus has the same units as pressure.
Dynamic viscosity has units Pa s = N m-2 s = kg m-1 s-1
= h-1 m-3, while fluidity has
units Pa-1 s-1 = h m3
and kinematic viscosity has units m2s-1 = c m.
Linear momentum has units kg m s-1 = h-1 m-1 while angular momentum in
kg m2 s-1 = h-1 m0 is unitless.
Power is measured in Watts with 1 W º 1 J s-1 = c m-2.
Since Ñ = åieiÐei has units m-2 on account of the reciprocal basis vectors,
and a potential fP is defined so that -ÑPf = F is a
force we see that potentials have units N m2 = (ch)-1 m0.
However, physicists typically regard potential as the spacial integration of force
and so measure it in joules , with electrical potential measured in Volts where
1 V = 1 J C-1 = (hc)-1 m-1 (10-7/2 (ch-1)½)-1
= 107/2 (hc-1)3/2 m-1 .
Resistance is measured in Ohms with
1 W º 1 V A-1 = 1 J s C-2 =
(hc-1) m-1 c-1 m 107 hc-1
= h2 c-3 m0 .
Capacitance is measured in Farads with 1 F º 1 C V-1
= C2 J-1 =
107 ch-1 hc m
= 10-7 c2 m .
The permitivitty of vacuum e0= (2hca)-1Qe-2= 8.85419×10-12 Fm-1 = (4p)-1 .
Inductance is measured in Henrys with 1 H = 1 m2 kg s-2 A-2
= 1 m2 kg C-2 = 107 m .
Non-S.I. Units
In atomic physics the electronvolt eV »1.60218×10-19 J » 1.78266×10-36 kg » 8.06554×105 m-1
is common, often as
mega-electronvolt 1 MeV = 106 eV
and giga-electronvolt 1 GeV = 109 eV .
From 1 m = (2p)-1hc(Mc2)2
we have
1 GeV
»
1.602×10-10 kg m2s-2
» 2-32.54 J
= 5.0632911 × 1015 m-1
» 252.17 m-1 » 280.33 s-1 .
1 eV =
1.602 × 10-19 J is considered a unit of energy. 1 GeV = 1.602 × 10-10 J and
1 J = 0.6242 × 1010 GeV.
1 eV c-1 » 5.36×10-28 kg m s-1 can be thought of as a unit of momentum.
1 eV c-2 »
1.78266175 × 10-36 kg can be thought of as a unit of mass.
[ The
c-2 is frequently ommitted in the literature, so that, for example, erroneous references to an
"electron mass" of 0.511 MeV rather than 0.511 MeVc-2 are woefully common
]
Other notable units are the mile (» 1609 m) ; the nautical mile (1852 m); the year
(31 556 926 s » 25106 s );
the light-year (» 9.4605284×1015 m » 1016 m);
and the parsec » 254.78 m .
Planck System
In Planck's system, one choses the basic length unit so as to unify the squared-length gravitational constant
Gc-2
» 6.674×10-11 m3s-2 kg-1
(2.988×108 m s-1)-2
» 2-33.80 (228.16)-2 m kg-1
» 2-90.12 m kg-1
= 2-231.14 m2
and our fundamental unit of length becomes
the Planck length lP = (hGc-3)½ = 1.61624×10-35 m = 2-115.57484 m, with associated Planck time c-1lP = 2-143.73423 s.
Note that G= 6.673×10-11 N m2 kg-2= 6.673×10-11 ch-1 (hc-1)2 m2= 1.47488×10-52 m2.
The Planck mass ((2p)-1 h G-1)½
» 2.176 45(16) × 10-8 kg
is the mass of a black hole with Schwarchild radius as the Compton wavelength.
. Multiplying by (8p)-½ gives the reduced Planck mass.
Notable lengths
Human physicists tend to work with (integer) powers of ten, ultimately because that is the number
of fingers possessed by the majority of them. It is easier and
more natural to work with (fractional) powers of two, since these can be more readily multiplied.
Based on the circumference of the Earth (the quarter latitude through Paris) the "arbitary" meter
length unit actually has much to commend it numerically. We note here
(novelly to the best knowledge of the author) that the electron Yukawa potential damping factor
Me- ch-1 = 6×262 m-1
to within 0.041%, a consequence of the bizarrely suggestive dimensionless
electroterran identity Me- R, h-1c » 1.00147 × 24×262×107
where
R, denotes the radius of the Earth
and Me- denotes the mass of the electron!
| Illustrative Lengths |
| Length ( m) | Example | | 2-115.575 | Plank Length c-1(hGc-1)½ | | 2-48.9192 | Heisenburg distance quanta 2Qe-2(3Me-c2)-1 | | 2-48.3343 | Compton Radius (Electron) (4pe0)-1 Qe-2(Me-c)-1 | | 2-42 | Gamma ray wavelength | | 2-38.5844 | Compton Wavelength (Electron) h(Me-c)-1 | | 2-34.1375 | Bohr Radius h(Me-ca)-1 | | 2-35.2193 | Hydrogen atom | | 2-34.9089 | Helium atom | | 2-33.2193 | 1 Angstrom (10-10 m) | | 2-31.4119 | C60 'buckyball' radius | | 2-33.9825 | (½h|Qe-|-1)½ | | 2-29.8974 | DNA helix radius | | 2-23 | Virus | | 2-21.2535 | Visible light wavelength (violet) | | 2-20.4461 | Visible light wavelength (red) | | 2-17.1242 | Human blood cell | | 2-16 | Silk fibre | | 2-12 | Dust mite | | 2-8 | Ant | | 2-3 | Mouse | | 20 | Human child |
| | Length ( m) | Example | | 21- | Human adult | | 25- | Blue whale | | 27 | Radio wavelength | | 29- | Tallest human buildings | | 213.1105 | Mount Everest | | 214.6096 | Olympus Mons (Mars) | | 222.6047 | Earth radius | | 226.0913 | Jupiter radius | | 228.1594 | Light-Second | | 229.3735 | Solar radius | | 234.0663 | Light-Minute | | 237.1223 | Earth orbit | | 239.9732 | Light-Hour | | 242.032 | Neptune orbit | | 244.5581 | Light-Day | | 253.0708 | Light-Year | | 255.2051 | Distance to Alpha Centuri | | 259.7147 | Light-Century | | 268.5285 | Radius of Milky Way Galaxy | | 274.3243 | Distance to Andromeda Galaxy | | 278.7028 | Distance to Virgo Cluster | | 280.6463 | Radius of Local Supercluster | | 286.6939 | Distance to Abell 1835 IR1916 Galaxy | | 289 | Human guesstimated radius of universe |
|
It is important to stress that one observer's radio wave is another's gamma ray in traditional relativity.
The faster an observer travels "with" the wave, the higher the percieved frequency. The faster he travels "perpendicular"
to the wave, the lower the percieved frequency. That said, visible light has a wavelength around
2-20 m (the size of a single biological cell)
and a frequency of around 3×1014 Hz » 248 Hz .
Gamma rays have a wavelength of order 10-12 m » 2-42 m
with a frequncy of order 270 Hz. Radio waves have wavelengths of order 27m
and frequency of order 231 Hz .
Atomic radii (orbital radius of electron) range from 2-49 to 2-47 m .
Current estimates are approximately 2226 atoms in our galaxy and 240
galaxies in the universe giving something in the order of 2266 atoms in the universe,
which is presently considered by Big Bangers to be 15 × 109 years » 8 × 1014 s » 249 seconds old
and roughly 296 m across.
The unit of atomic mass is approx 2-89 kg » 252 m-1 while
the mass of the electron is roughly 0.511 MeV c-2 » 2-10.93 GeV c-2
» 2-99.79 kg
= 241.23 m-1 .
Time Quantisation
Some authors (eg. Hotson) suggest time is quantised in units of t = 2Qe-2(3Me-c3)-1 » 6.26642×10-24 s = 2-77.078633 s with associated Heisenberg length 2Qe-2(3Me-c2)-1 =1.87863×10-15 m = 2-48.91924 m . This is proportion 4Qe-2(3hc)-1 » 9/925 of the electron zitterbewegung period (2Me-c2)-1h = 6.44044×10-22 s = 2-70.395259 s .
The universe is considered to be about 13.7×108 years = 258.5849 s » 2135.664 t and the furthest known galaxy is approx 2135.613 c-1t away.
Conclusions
Via c and h (with temperature also requiring kB),
charge, angular momentum, speed, resistance, permitivity and pemeability can
all be asigned unitless values; length, time, inductance, capacitance, and kinematic viscosity can be measured in length units
such as the meter m ;
mass, energy, temperature, electric potential, current, and linear momentum can then be measured in m-1 ;
power can be measured in m-2;
dynamic viscosity in m-3;
pressure and density in m-4.
More generally, any scalar physical quantity may be expressed in the form
a mb where a and b are real numbers, b usually rational
and typically an integer,
Any reference length unit suffices and the implications for simple and robust programming and data type strategums are profound.
However, even though, say, momentum and temperature can both be measdured in m-1 they are not the same thing
and it far from clear that they can be
anymore meaningfully added when both in m-1 than when expressed in kg m s-1 and K.
Typically the units of a value are implicitly implied by the program context rather than explicitly stored with the value
but a natural way to represent a composite unit is as a reference length power and the powers of c, _placnk, and kB respectively so that momentum would be
(-1; 0, -1, 0) and temperature (-1;-1,-1,1) . Length is (1;0,0,0) and charge (0;-½,-½,0). These powers will typically be
small integer multiples of ½ so we might allocate four bits to each and represent physical units with 16-bit words.
If we represent lengths in a fixed point meter value with fourteen fractional binary bits
then a 32 bit intger can hold lengths in the range
±217 m » 131 km » 2-11 light-seconds to within
2-14 m » .06 mm. This is adequate for a human city but not for the Earth, let alone
the solar system so if we are to used fixed point it is natural to use 64-bit integers taking us to
±249 m to the same .06 mm accuracy; which gets us out past Pluto
but not to Alpha Centuri. For a fixed point Galactic simulation 96 bits are adequate but if
we wish to go down to Compton radius accuracy we approach 118 bit.
The visible universe at Compton resolution requires 138 bits and if we wish to work in Planck lengths we are looking at 205.
All this suggests that a 256-bit (32-byte) integer data type would amply suffice for individual properties
of particles and for a particle "ennumeration index" when simulating an isolated galaxy
without recourse to hierachical coordinate systems, but that two or more further bytes
would be needed to ennumerate particles in a multigalactic simulation.
This exludes photons, however. A 60W lightbulb emmits 266 photons per second, the sun roughly 2148 .
Glossary
Contents
Author
Copyright (c) Ian C G Bell 2006
Web Source: www.iancgbell.clara.net/maths or
www.bigfoot.com/~iancgbell/maths
Latest Edit: 20 Mar 2007.

