Rigid Body Moving Through a fluid
Suppose we have a solid N0-D body B with surface (N0-1)-curve dB moving with stance bivelocity W
through a fluid which we assume to be at rest prior to the passage of B. We expect B to leave a
kinematic disturbance (or "wake") in the fluid,
losing kinetic enregy in the process.
Even if the flow is irrotational, for N0=2 there can be nonzero circulations about circuits that enclose
B.
For concreteness let us consider an aircraft Q flying over a city 4. The aircraft has
stance S4¬Q and 2-vector bivelocity W4=-2S4¬QS4¬Q·
and we assume for simplicity that the atmospheric flow vp4 at a given event p due to wind, thermals, flak and so forth
varies only slightly at the scale of the aircraft so that we can embody the motion of the atmosphere encountered by the
plane by a single wind velocity 1-vector w4(c) where c is the instantaneous position of
the mass centre of the plane .
It is convenenient to cast aircraft bivelocity W and the wind velocity w into the frame of the aircraft and consider the
aircraft to be travelling with bivelocity W+ = WQ - wQe¥ through a fluid at rest.
We choose Q coordinates such that the aircraft is (approximately) symmetrical in the y=0 plane with e1 coresponding to "forward",
e2 to "left" and e3 to "up". We expect the velocity component of W+ = WQ - wQe¥ to approximate a positive multiple of e1e¥
but have some smaller "sideslip" and "drop" e2e¥ and e3e¥ components.
The 2-vector biimpulse T(W+) imparted by the fluid to the aircraft is dependant solely on the surface geometry of the
aircraft and is generally not linear in W+; indeed it tends to have quadratic form
T(lW+) = l2T(W+)
since if we double W+ then in small time interval dt we encounter twice as many fluid particles each of which has
twice as much momentum relative to the body.
In reality, aerodynamic properties vary with higher mach speeds so we do cannot characterise
T purely "directionally" via
T(W+) = |W+|2 T(W+~) .
However, classical aerodynamic theory usually formulates the force on the body solely due to its velocity
as T
= åi<jv2 Cij(v~Q) eijW
where the ½N0(N0+1) direction-dependant scalar coefficients can be reagrded as coordinate in the wind frame having
e1W = v~ ;
e2W = ¯v*(e2Q) ;
e3W = ¯v*(e3Q) .
Direction v~Q is typically parameterised by aerodynamic angles
a =
tan-1(e3Q¿v~
(e1Q¿v~)-1) and b= sin-1(e3Q¿v~) .
Bivectors W+ and T(W+) each have ½N(N+1) coordinates since W+ resides in e¥*
while T resides in e0*.
Thus expressing each T coordinate as a general quadratic form of the W+ coordinates requires
(½N(N+1))3 scalar coefficients. This is 27 for N=2 and 216 for N=3.
Consider approximating
T(W+) as åk=1K
(W+¿ak)Ù(W+¿bk)
for 2K 3-vectors a1,b1),...,ak,bk).
imparted by the fluid to the aircraft is dependant solely on the surface geometry of the
 Fluid Mechanics
Fluid Mechanics
Introduction
To model the motion of a body through a fluid medium such as air or water we must at least approximate the
effects of the fluid on the body which requires simulation at least in part of the motion of the fluid, which is likely to be complicated and frquently chaotic.
Classical Flows
Classical fluid mechanics typically represents a flow of matter by a ÂN0 nonunit 1-field
where N0 is the number of spacial dimensions with MP representing at a given time t the total momentum per unit
volume passing through a small test volume at spacial position PÎÂN0;
together with scalar 0-field mP representing the density (mass per unit volume) at P (as measured over a small
test volume) , constant for an incompressible fluid. We have Mp = mpVp where
Vp=mp-1Mp is the (nonunit) average spacial velocity vector of the matter at
p= P+te4 is an N=N0+1 dimensional spacetime event. Vp is undefined when mp=0.
In thermodynamics we also consider the matter at p to have scalar temperature Qp.
The flow satisfies the conservation of matter law (aka. a continuity equation)
if
ÑP¿Mp = -¶mP/¶t = 0
which states that the ammount of matter leaving a small region of volume V at P per unit time
as measured over a small test interval equals the fall
in the ammount of matter mPV at V at P per unit time
We can express the matter conservation law
as
¶ mP/¶ t + ÑP¿(mpVp)
= ¶ mP/¶ t + (Vp¿ÑP)mpÑ
+ mp(ÑP¿Vp)
= ((¶ /¶ t) + (Vp¿ÑP))mp
+ mp(ÑP¿Vp)
= 0
where (¶ /¶ t) + (Vp¿ÑP)
is known as the substantial derivative
corresponding to the rate of change when "following" the flow. Note that this represents the derivative in the direction of the flow
scaled by the speed of the flow.
If we define ÂN 1-vectors
p=P+te4 and vp=Vp±e4 where N=N0+1 and e4 is a (non-relativistic) "temporal" axis perspendicular to
ÂN0 with e42=±1 then the substantial direction becomes
(vp¿Ñp) with the differentiating scope of the Ñp extending only rightwards rather than encompassing the vp.
For a steady flow Mp = MP with vanishing Ðe4 derivatives
the matter conservation law becomes
(Vp¿ÑP)mpÑ + mp(ÑP¿VpÑ) = 0
and for an incompressible flow with mp=m>0 this yields the incompresability condition
ÑP¿Vp = 0, ie. the spacial divergence of the N0-D velocity 1-vector is zero.
For vp=Vp±e4 , the incompressability condition is Ñp¿vp=0.
For an incompressible flow "momentum" and "velocity" fields become effectively equivalent with
Mp=mVp.
Classical Pressure
The scalar static pressure sp at p is independant of the macroscopic "net flow" mp at p ,
and stems instead from microscopic "thermal" agitatation of the particles "at" p .
The use of the term "static" here is traditional, and relates to "pressure not due to flow" rather than a restriction on
the variability of sp with p. The pressure sp at p the sum of the static pressure and pressure due to the fluid motion,
Consider a small Â3 3-simplex or 2-sphere V centred at p in a fluid at rest from within which the
fluid has been removed. Random microscopic thermal motion of the fluid will tend to cause molecular impacts
on the surface of the simplex which we can regard as imparting locally normal "inward" momentum uniformly across the boundary surface.
Integrating this inward component across the surface and dividing by the surface area content leads us to
scalar pressure which we can regard as the magnitude of the thermal e4-forces exterted across a small 2-simplex
or 1-sphere centred at p of aribitary 2-blade tangent, divided by the simplex area.
For N0||>3, scalar sp represents the inward thermal forces across a (N0-1)-sphre.
In an anisotropic ideal gas spV is proportional to nQp where V=|V| is the volume
of a test 3-simplex V at p containing n molecules of average temperature Qp. n is proportional
to total mass mpV so sp is proportionate to mpQp and we usually write
sp = RmpQp where R is the gas constant for the fluid.
The entropy proportionate to (spmp-g)↓
= sp↓ - gmp↓
where dimensionless g is the specific heat ratio
is conserved by fluid elements in the absence of heat conduction so that (vp¿Ñp)spmp-g = 0
. Entropy has units ( m-4)↓ so can be measured in m↓
.
Now consider some fluid inside V. The total forces acting on this fluid are
the external macroscopic forces
òV |d3p| fp
where fp=mpgp + hp is e4-spacial forces exerted
(typically we might have gp=-ge3 for uniform vertical gravity)
,
and the static pressure integrated over the boundary
òdV|d2p|(-np)sp
= -òdVd2p e123-1sp
= -e123-1 òVd3p ÑPsp
where np
= I2p-1 e123
= I2p e123-1
is the outward normal at p Î dV .
Classicists typically asssume gp=-ÑpGp and hp=-ÑpHp derive from gravitational and
nongravitational scalar 0-potentials.
The total change in momentum incured by the mass mp|V| of fluid as it follows the flow lines
is
òV d3p (ÑP¿vp)mp so we have
(ÑP¿vp)mp = mpgp + hp - Ñpsp which for constant density mp=m simplifies
to the momentum conservation law
(vp¿ÑP)vp = gp + m-1hp - m-1(ÑPsP)
aka. Euler's equation when combined with ÑP¿VP=0 .
For P in Â3 we have
(Vp¿ÑP)VpÑ = ½ÑP(Vp2) - Vp×(ÑP×VpÑ)
so we can express the momentum conservation law as
½ÑP(Vp2) - Vp×(ÑP×VpÑ) + m-1ÑPsp -
m-1fP = 0 .
[ Proof :
a×(b×c) = (a¿c)b - (a¿b)c Þ
Vp×(ÑP×Vp) = (Vp¿ÑP)VpÑ - (Vp¿VpÑ)ÑP
= (Vp¿ÑP)VpÑ - ÑP(VpÑVp)
= (Vp¿ÑP)VpÑ - ½ÑP(Vp2)
.]
Small peturbation sound waves
Let scalars pressure sp = s0+sp and density mp=m0+mp be small deviations from s0 and _wasmup0
Since entropy (spmp-g)↓
= (s0+sp)(m0+mp)-g)
= _presp0m0-g Þ (1+s0-1sp)(1+m0-1mp)-g = 1
which to first order in s0-1sp and m0-1mp
is sp = s2mp where s=
(m0-1s0g)½ .
Now let us suppose that Vp is small so that the
matter conservation law
mp· = -(Vp¿ÑP)mp - mp(ÑP¿Vp) reduces to
mp· = -m0(ÑP¿Vp) giving
(ÑP¿Vp) » -m0-1mp· .
The
momentum conservation law linearises
to ÑPsp =
(mp+m0)gp + hp
- (mp+m0)Vp· »
(mp+m0)gp + hp
- m0Vp·
which gives
ÑP2sp = (ÑP¿)((mp+m0)gp + hp - (mp+m0)Vp·)
= (ÑPmp)¿gp - m0(ÑP¿)(Vp·)
= (ÑPmp)¿gp - m0(ÑP¿Vp)·
= (ÑPmp)¿gp + (mp·)·
= (ÑPmp)¿gp + (s-2sp·)·
Þ
sp·· = s2ÑP2sp so the pressure and desnity perturbations
satisfy the standard 3D wave equation with radial solution
sp = r-1(F(r-st)+G(r+st)) corresponding to an outward wave of amplitude F
of radial speed s and an inward wave of amplitude G and radial speed -s.
s=(m0-1s0g)½ thus corresponds to the propagation
speed of density and pressure perturbations from steady state values m0 and s0 and is known as the speed of sound
in the fluid.
Navier-Stokes
Suppose we combine the static pressure force -spnp with a viscous force
u((np¿Ñp)mpÑ + Ñp(np¿mpÑ))
; reducing to um((np¿Ñp)vpÑ + Ñp(np¿vpÑ))
when mp=m.
If we regard np as varying negligibly with p compared to the variation of vp
(eg. when over a flat surface) then we can view this as the np directed flow derivative plus the gradient of the np-directed flow-speed, equally wieghted
by scalar u, leading to the Navier-Stokes equation
(vp¿Ñp)mp
= -mp(ÑpGp) - (Ñpsp) - (ÑpHp) + (vp¿Ñp)mpÑvp
+ uÑp2mp .
For incompressible flow mp=m this becomes
(vp¿Ñp)vp
= -(ÑpGp) - m-1((Ñpsp) + (ÑpHp)) + uÑp2vp
where scalar u is the kinematic viscosity. Water has kinematic viscosity 10-6 m2s-1
at 15 oC while air is fifteen times that, olive oil a hundred. Treacle has viscosity of roughly 1.2×107
m2s-1 at 15 oC, falling rapidly with temeprature.
Vorticity
For an incompressible flow under gravity, Navier-Stokes becomes
(Ñp¿vp)vp = -ÑpGp - m-1((Ñpsp)
+ uÑp2vp
and since (vp¿Ñp)vp = vp¿(ÑpÙvp) + ½Ñp(vp2)
we have vp¿wp = -ÑpEp + uÑp2vp where
Ep = ½vp2 + Gp + m-1sp
and wp º ÑpÙvp has Ñp¿wp=0.
Hence
ÑpÙ(vp¿wp) = uÑpÙ(Ñp2vp)
= uÑp3.vp .
But ÑpÙ(vp¿wp) =
(Ñp¿(vpÙwp))i where
(N-2)-vector kinematic vorticity wp º wpi-1 = (ÑpÙvp)* so we have Ñp¿(vpÙwp) = 0
[ Proof :
ÑpÙ(vp.wp) = (Ñp¿(vpÙ(wpi-1)))i
= (Ñp¿(vpÙwp))i
.]
For incompressible flow,
Ñp¿(vpÙwp)
= (vp¿Ñp)wpÑ
- vpÑÙ(wp.Ñp)vpÑ
so we have
geometric vorticity equation
(vp¿Ñp)wp
= (wp.Ñp)Ùvp + u Ñp¿(Ñp2vpi-1)
with the differentiating scope taken rightwards only.
For N=3 inviscid flow (u=0) this reduces to
(vp.Ñp)wp = (wp.Ñp)vp with 1-vector vorticity wp = (ÑPÙVP)* = ÑP×VP and is known as the third Helmholtz vortex theorem.
[ Proof : (vp¿Ñp)wpÑ
+ (Ñ¿vpÑ)wp
- vpÙ(Ñp¿wpÑ)
- vpÑÙ(Ñp¿wp)
reduces to result since Ñp¿wp = ÑpÙwp = ÑpÙÑpÙvp vanishes as does
Ñp¿vp .
Also u(ÑpÙ(Ñp2vp))i-1
= u(Ñp¿((Ñp2vp)i-1)
.]
Thus for N0=3 the flow-directed derivative of the vorticity (vp¿Ñp)wpÑ equals the
vorticity-directed derivative of the flow (wp¿Ñp)vpÑ ;
while for N0=2 steady flows we have scalar vorticity preserved along streamlines
(ÑP¿VP)wp=0 since (wp¿Ñp)vp=wÐe3vp=0.
When fp=0, integrating along a streamline gives
Bernoulli's equation sp + ½mvp2 = s0 ,
where scalar s0 is known as the stagnation pressure.
Bernoulli's equation applies when mp is constant and the flow is static. More generally
Ep = sp + mGp + Hp + ½mvp2 is constant along the streamline if mp=m and wp=0 along it.
[ Proof :
sp1 = sp0 + òt0t1 dt vp¿(Ñpsp)
= sp0 + òt0t1 dt vp¿
(-mp(ÑpGp) - (ÑpHp) - (Ñp¿vp)mpÑvp -
mp(Ñp¿vp)vp )
= sp0 + m(G0-G1)
(H0-H1)
- m òt0t1 dt vp¿((Ñp¿vp)vp )
= sp0 + m(G0-G1)
(H0-H1)
- m òt0t1 dt vp¿(vp¿wp + Ñpvp2 )
= sp0 + m(G0-G1)
(H0-H1)
+ ½m (v02 - v12) .
Hence sp + mGp + Hp + ½mvp2 is constant along the streamline.
.]
Circulation
The geometric M-circulation about a closed M-curve CM of a flow mp=mpvp
is the <M-1;M+1>-vector GC1 º òCM dMp vp .
Circulation is thus usually considered to be an integration of velocity rather than momentum and so has units
mM+1 s-1.
The 1-circulation about a closed 1-curve (ie. a loop) C1
is thus the <0;2>-vector GC1 º òC1 dp vp
and the term circulation traditionally refers to the scalar part
GC1 º òC1 dp¿vp .
For N0=2, C1 bounds a "solid" flat surface region C2 and for an irrotational flow with
vp=Ñpfp
defined over C2 we have
GC1 º òdC2 dp vp
= òdC2 dp Ñpfp
= òd2C2 d0p fp = 0 .
Hence for N0=2 the scalar circulation vanishes provided the region enclosed
by C1 contains no regions absent of flow or at which ÑpÙvp is nonzero. In particular the scalar circulation around a
solid lamina need not vanish, but is independant of enclosing path C1. Similarly a vortex point with nonzero ÑpÙvp within C2 will contribute a fixed
"residue" circulation independant of the enclosing path.
|&| òC2fp|d2p| .
The geometric generalisation of Stoke's law
òdCN0-1 dN0-2p.¦(p)
= (-1)N òCN0-1 (ÑÙ¦(pÑ)).dN0-1p
means that the (N-3)-vector component of the (N0-2)-circulation around the (N0-2)-curve boundary of an
open hypercurve CN-1 over which
vp is defined equals the vorticity integration over CN0-1
(-1)N0 òCN0-1 (ÑÙvp).dN0-1p .
Thus if vp is defined and irrotational over CN0-1 the (N0-3) component of GdCN0-1
vanishes.
Thus for N0=3 we have
GdC2 º òC1 dp¿vp
= -òC2 (ÑÙvp).d2p
and so if GC1 is nonzero for a closed 3D 1-curve (ie. a path loop) and C2 is any
3D hypercurve spanning (bounded by) C1 over which vp is everywhere defined, then vp must be irrotational over one or more
regions of C2.
If CN0-1=dCN0 is the hypercurve boundary of an open set CN0
over which vp is defined
then the <N0-2;N0>-vector hypercirculation GCN-1
º òCN-1 dN-1p vp
= òCN dNp Ñpvp
vanishes for a static incompressible irrotatuonal flow with Ñpvp=0.
If CN containis regions over which vp in undefined or zero then
GCN-1 may be nonzero but tends to be indendant of CN-1
in that we can deform CN-1 without altering GCN-1 provided we do not move
CN-1 across any undefined vp regions .
The hypercirculation about a (N0-1)-curve CN0-1 is the <N0-2;N0>-vector
GCN-1 º òCN-1 dN-1p vp
=
òCN0-1 ((-1)N0-2 ¯dN0-1p(vp) _dNm1 + (-1)N-1^dN0-1p(vp) dN0-1p)
= (-1)N0òCN0-1 (¯dN0-1p(vp) - ^_dN0m1(vp)) dN-1p
= (-1)N0
(òCN0-1 ¯dN0-1p(vp)¿dN0-1p)
- òCN0-1 ^dN0-1p(vp)ÙdN0-1p)
.
When vp=Ñpfp the (N0-2) component
òCN0-1 ¯dN0-1p(vp)¿dN-1p
= òCN0-1 ¯dN0-1p(Ñpfp)¿dN0-1p
= òCN0-1 (¯dN-1p(Ñp)fp)¿dN0-1p
º òCN0-1 (Ñp[CN-1]fp)¿dN0-1p
= òdCN0-1 fp dN0-2p
vanishes for closed CN0-1 (or has a constant (N0-2)-vector value comprising residues at enclosed poles).
The pseudoscalar hypercicrulation component
òCN0-1 ^dN0-1p(vp)Ù_dN0m1
= i òCN0-1 (vp¿np)|_dN0m1|
measures the outflow across CN0-1 and vanishes for a steady incompressable flow.
Otherwise for small |CN0-1| it approximates
i|CN0-1|(ÑP¿Vp) =
i|CN0-1|ÑP2fp evaluated at any particular p enclosed by CN0-1.
Reynolds Number
It is frequently the case in Navier-Stokes dynamics that one of (vp¿Ñp)vp and uÑp2vp will dominate to
the extent that the other may be neglected and far simpler equations solved. The Reynolds number
u-1ua where u is a typical flow speed and a a characteristic length for the problem
provides a rough indicator of the likely ratio of the magntiudes of the inertial (vp¿Ñp)vp term to the viscous uÑp2vp term;
a high Reynold's number favouring the inviscid approximation forcing u=0.
This can fail when the large second derivatives present in thin boundary layers "seperate" from the boundary and signifcantly effect the flow far from the boundary.
Complex Potential
The complex potential is used to emulate incompressable, irrotational, usually steady, Â2 planar flows.
Stream Function
Setting scalar stream function yp º
òC dV2 V1
- òC dV1 V2 for any Â2 path C from 0 to p
yields
V1 = Ðe2yp ; V2 = - Ðe1yp ; ie.
Vp = e12(ÑPyp)
= (ÑPyp)e12-1
= Ñp×(ype3)
= (ÑPÙ(ype3))e123-1
with Vp2 = (Ñpyp)2 .
If yp is any analytic real scalar field over Â2
satisfying this then its analyticity provides incompressability condition Ðe1V1 + Ðe2V2 = 0, ie.
ÑPVp=0 and also Ñp2yp = 0.
Hence Vp = (ÑP(ype3))e123-1 = -ÑPype12 .
Vp2 = (Ðe2yp)2 + (-Ðe1yp)2 = (Ñpfp)2
Also note that ÐVp yp = (Vp¿Ñp)yp = 0 so yp is constant when following the flow.
Such 1-curves along which yp is constant are known as streamlines.
Velocity Potential
For a steady irrotational incompressible flow with ÑpÙVp = 0 we can constuct a 0-potential
fp = òC dp¿Vp for any path C from 0 to p so that Vp=Ñpfp , ie.
Vi = ei2Ðeifp . If the flow is conserved we also have Ñp¿Vp=0 so ÑpVp =
Ñp2fp = 0.
Setting Fp º fp(ÑPfp) we have
ÑPFp = (ÑPfp)2 + fpÑP2fp = (ÑPfp)2
= Vp2 hence for constant density flow the kinetic energy within a volume
½mòV d3p VP2 =
½mòdV d2p fp(ÑPfp)
with pseudoscalar part giving divergence theorem
½mòV |d3p|VP2
= -½m òdV|d2p|fpÐnfp where n is the outward normal to the (N0-1)-curve
integration surface dV .
Thus in an incompressibe incompressable flow, we can deduce the kinetic energy insode a volume of fluid
from fpÐnfp over the blundary of V
Complex representations of 2D Flows
When N0=2 then by taking i=e21=-e12 and setting z = pe1 = x1+x2e21 = x1+x2i ; v(z) = Vpe1 = V1+V2e21 ;
we can work in commtuing algebra C @ Â2 +.
We define automorphic conjugation x^ º e1xe1 negating e2 and e12 but preserving 1 and e1 so
corresponding to complex conjugation over Â2 + and reflection in x2=0 over Â2, giving innerproduct
a.b = Real(a^b) and a2 = a^a =
|a|+2 .
Complex Potential
The Complex 0-potential fp º fp + iyp
satisfies ÑP2fp = 0 since
ÑP2fp and ÑP2yp both vanish.
It is defined for x=P where P Î ÂN0=Â2
but by defining z=x1+ix2 = pe1 where p=x1e1+x2e2
and taking i=-e12 we can regard
fp = fz,t as a t-dependant regular function mapping C®C
whose conjugated derivative provides flow v(z) = Vpe1 = f'(z)^ .
By virtue of its construction, the complex potential satisfies the
Cauchy-Riemann equations
and so any regular complex function provides a complex potential
with a direction-independant derivative f'(z,t) º (d/dz)f(z,t) =
df/dx1 + idy/dx1 =
V1 - iV2 = v^(z,t) .
Hence Vp = f'^ = f^' where ' denotes regular differention with resepect to z
and so Vp2 = |f'(z)|+2 .
A regular complex 0-potential fp(t) with Ñp2fp=0 thus fully embodies an incompressible irrotational 2D flow
with spacial derivative f' equal to the complex conjugate of the flow, and streamlines indicated by
constant Imag(f). If fp is independant of t then the flow is steady.
Apart from at z=0, the reciprocal potential fp(t)-1 is also regular
with (fp(t)-1)' = -fp(t)-2 f'p(t) . The
fp(t)-2 factor is complex and both redirects and rescales the derivative.
Similarly f(lza) has flow
(f'(lza)la za-1)^ which is
(la za-1)^ times the flow due to f(z).
For a=-1 we have f(lz-1) giving flow
-(lz-2)^ times the flow due to f(z).
Example: Uniform Flow
The uniform flow of speed A and direction subtending a with the horizontal is given by
v(z,t) = a = A(ia)↑
and has fp = a^ z = A(-ai)↑ z
where p=(x1,x2)=[r,q] and z=x1+ix2.
Example: Line Vortex
Consider the circular flow up = gr-1eq , ie.
v(z,t) = g|z|+-2iz
= gi(z-1)^
= (-giz-1)^
having circulation
2pg
|+ e12 ò0a dz ò02p dq gq z
= 2pg(1+ e12½pa2).
.
yp=-gr↓ while the velocity potential is fp=gq yielding
fp
= -gi(z)↓
Setting G=2pg we have line vortex potential
fp = G(2pi)-1(z)↓ with circulation
G(1+e12½pa2) about any loop enclosing r=a
and associated flow up = (2p)-1Gr-1eq tending to zero at r=¥ .
.
The r-1 factor on the speed means that the angular momentum mppÙVp = mpgereq
= mp(2p)-1Ge12
= mp(2pi)-1G
about 0 at p is independant of p for incompressible flow mp=m.
Note that f(lz-1) = G(2pi)-1(l↓ - z)↓
is the potential for circulation -G plus an irrelevant constant.
For large D, fp = G(2pi)-1(z-D)↓ approximates uniform flow
v(0)^ = (2p)-1GD-1i(-D)~
= (2pi)-1GD-1 so
fp = a^D(z-D)↓ provides flow close to
a for r<<D.
Uniform Â2 Flow Past a Circular Boundary
If f(z) is the complex potential of a flow having no singularities for |z|<a
then
f(z) + (f(a2z^-1))^
= f(z) + (f(a2|z|+-2z))^
has the same singularities as f(z) over |z|>a
and is purely real when |z|=a (ie. yp=0 when r=a), so the circle r=a
is a streamline.
From this we deduce that
f(z) = a^z + (a^a2z^-1)^
= a^z + aa2z-1
has flow f'(z)^ approaching
a for large r but with zero er component when r=a .
By adding a line vortex potential
f(z,t) =
a^(z-c) + a2a(z-c)-1
+ G(2pi)-1 (z-c)↓
= A((-ai)↑(z-c) + a2(+ai)↑(z-c)-1) + alai-1(z-c)↓)
where
a=A(ai)↑ and
dimensionless
scalar
l º lr º l(r,G,A) º (2pr)-1 A-1 G
= r-1ala
we obtain the complex potential for a flow
v(z) = f'(z)^
= A((ai)↑ - a2(z-c)-2^(-ai)↑)
- G(2pi)-1(z-c)-1^
= A((ai)↑ - a2(z-c)-2^(-ai)↑
+ alai(z-c)-1^ )
that approaches uniform flow a=A(ai)↑ as r®¥
but has circle r=a as a y=G(2p)-1a↓ streamline.
Taking a=0, c=0 for a uniform horizontal flow Ae1 at infinity
around the origin centered circle we have
f(z) = A(z+a2z-1) + G(2pi)-1 z↓
= A(z+a2z-1 + ala z↓ i-1)
= A(r(iq)↑ + r-1(-iq)↑a2) ) + G(2pi)-1(r↓+qi)
= Ar(1+(r-1a)2) cos(q) + (2p)-1qG
+ Ar(1-(r-1a)2) sin(q)i - (2p)-1r↓Gi
so our a=0 scalar potential and stream functions are
f(r,q) = Ar(1+(r-1a)2) cos(q) + (2p)-1qG ;
y(r,q) = Ar(1-(r-1a)2) sin(q) - (2p)-1r↓G .
Vp = A( (l - (1+(r-1a)2) sinq)eq + (1-(r-1a)2) cosqer ) .
Vp2
= A2 ( l(r)2 - 2l(r)(1+(r-1a)2) sin(q) +
1+(r-1a)4-2(r-1a)2 cos(2q) ) .
f(lz-1)
= A((lz-1)+a2(l-1z)
- ala z↓ i-1)
+ ala l↓ i-1)
provides a flow of strength
Aa2l about a circular boundary of radius la-1
with circulation -G.
Along the boundary r=a we have constant
y = -(2p)-1a↓G and
Vp = A(l(a) - 2 sinq)eq parallel to the boundary as required
and vanishing at two stagnation points q= sin-1(½l(a)) providing
l(a)<2 (ie. G < 4paA) .
For l(a)>2 we have just one stagnation point at q=±½p
provided l(r) = ±(1+(r-1a)2)
Û (r-1a)2 ± l(a)(r-1a) + 1 = 0
Û (r-1a) = ½(-/+ l(a) ± (l(a)2-4)½)
Û (r-1a) = ½l(a) + ((½l(a)2-1)½ .
| 
|
[ Proof : Vp = -ÑPfpe12 = - (erÐer+eqÐeq)fpe12
= -(er¶/¶r+eqr-1¶/¶q) f(r,q,t)e12
= -er(A(1+(r-1a)2) sin(q) - (2p)-1r-1G)e12
+ -eqA(1-(r-1a)2) cos(q)e12
.]
Analytically we will consider the generalised circular flow
f(z) = ab(z-c) + a2a^b-1(z-c)-1 + G(z-c)↓ + Gb
with
f'(z) =
ab - a^a2b-1(z-c)-2 + G(z-c)-1
and
f"(z) =
2a^a2b-1(z-c)-3 - G(z-c)-2
but in practical cases we require purely imaginary G since the multivalued imaginary component
of z↓ = r↓ + qi makes for disconnected streamlines if left within y.
Further, we only have a y(z) = Imag(G)(r↓) circular streamline if
b(z-c) = (a2b-1(z-c)-1)^ which requires
a2 = |b|+2|z-c|+2
so we invariably take take a2=a2 positive real.
The total force exerted on the r=a boundary by the fluid is -mAGe2,
or more generally
mAGae12-1 where
a=ae1=A(ae21)↑e1 is the background flow.
[ Proof : Around the r=a streamline we have
Vp2 = A2(la - 2 sin(q))2
and in the absence of gravity (Gp=0) and other forces (Hp=0) we have
s0 = sp + ½mvp2
Þ m-1sp = m-1s0 - ½Vp2
= m-1s0 -
A2(½la2 + 2la sin(q) - 2 sin(q)2) .
The force exerted on a small element of the boundary is -spa dqer having e2 component
-sp sin(q)a dqe2 and integrating this around the boundary gives
zero total e1 force component and a total e2 force of
-m ò02p dq a sin(q)
A2(½la2 + 2la sin(q) - 2 sin(q)2)
= -maA22la ò02p dq
sin(q)2)
= -2pamA2la
= -mAG
.]
Thus there is no "drag" on a circular boundary in a steady uniform inviscid incompressible irrotational flow.
In reality there is drag, of course. Partly because actual flows are viscid but mostly because they are
unsteady and rotational.
Circular Â2 Flow Past a Circular Boundary
Taking f(z) + f(a2z^-1)^
= f(z) + f(a2|z|+-2z)^
= f(z) + f(a2|z-1)^
for fp = a^D(z-D)↓ provides
fp = a^D(z-D)↓
+ (a^D(a2z-1-D)↓)^
= a^D(z-D)↓
+ aD^((a2z-1-D)^)↓
f(z) = b(z-a)_logncj + G(z-c)↓
has v(0)
= -(ba-1 + Gc-1)
= a^ provided
b = a(Gc-1 - a^) .
Taking a muich larger than c so that the
a(Gc-1 - a^)(z-a)↓ term
approximates constant flow a^ near 0 and c .
ÂN flow around hypershpehrical boundary
An analagous result for N>2 is that
y(p) = ½(f(p-c) + (f(aN-2|p-c|2-N(p-c))»)
has Ñy(p) = ½(Ñf)(p-c)
+ ½aN-2|p-c|2-N(Ñf)(aN-2|p-c|2-N(p-c))»
since Ñ|x-c|2-N vanishes.
Over |p-c|=a we have
y(p) = ½(f(p-c)+(f(p-c))»)
and Ñy(p) = ½((Ñf)(p-c) + ((Ñf)(p-c))») .
Biimpulse exerted on a 2D boundary
The D'Alembert paradoxical result of zero drag in an inviscid incompressible steady flow around a circular boundary extends to general 2D boundaries
and provides that the force exerted on a 2D body by uniform (at infinity) flow v is
rGe12v perpendicular to v.
Thus for steady inviscid irrotational flow the shape of the 2D boundary is irrelevant to the direction of
the force, but determines its magnitude by fixing the scalar circulation G.
Force perpendicular to fluid velocity is known as lift reagrdless of whether it is "up" or "down"
with regard to e3Q or gravity, eg. a diving plane "lifts" horizontally,
and F=rGe12v equivalent to F=-rGiv is known as the Kutta-Joukowski Lift Theorem.
Since the force derives from the pressure which is determined by Vp2, the lift remains the
same if we negate the flow, with both v and G changing sign.
Suppse we have a 2D 1-loop C=p(t) where tÎ[0,L] of total length L that is the y=y0 streamline of a steasdy flow.
At a point p(t) = ze1 on the boundary C we have a velocity Vp=ve1=f'(z)^
and force element dF =
-spe21dp
= (½rpVp2 - s0)e21dp
= ½rpVp2e21dtVp~ - s0e21dp
= ½rpv^ve21dtv~e1 - s0e21dze1
= -½rpv2v^~e2dt - s0e2dz^
= -½rpv2dz^e2 - s0e2dz^
Complex force dF =
dFe1 =
-½rpv2dz^i - s0idz^ with conjuate
dF^ =
½irp(v^2)dz + s0dz
= ½ir(z)f'(z)2dz + s0dz
so the net conjugate force exerted on the boundary is
òC dF ^ =
½iròC dz f'(z)2 , which is known as Blasius's Theorem.
If f'(z)2 is expressed as a Laurent series
f'(z) = åk=-n¥ ak(z-c)k
for n³1 about some c then traditional complex residue calculus
provides òC dz f'(z)2 = 2pia-1 ,
though of course if there are multiple poles inside C we have multiole contributory residues.
The moment of dF about c is (p-c)ÙdF = ((p-c)dF)<2> -
= ((z-c)e1dFe1)<2>
= ((z-c)(dF)^)<2> so the total moment about c is
(½iròC dz (z-c)f'(z)2)<2>
= ½irReal(òC dz (z-c) f'(z)2 )
= ½irReal(2pia-2)
= -pirImag(a-2)
in the event of a single pole at c.
Unlike the lift, the torque does not in general vanish when G=0.
The deflector or stress tensor
vpup-1 deflecting bivelocity up to bivelocity
vp is naturaly parameterised over complex time as
(t(vpup-1)↓)↑ up .
Letting
up(t) = (t(t)(vpup-1)↓)↑ up
where t(t) is a path from t(T) to t(T+d).
The aerodynamic profile of a body at a particular mach speed S
can be characterised by directonal deflection rp_vdp_udin
Conformal flow warping
Given a conformal map Z = f(z) and a complex potential f(z) we have complex potential
F(Z) = f(f-1(Z)) defining a flow in the "warped" Z space
V(Z) = F'(Z)^ º dF/dZ^
= (df/dz dz/dZ )^
= (df/dz (dZ/dz)-1)^
= v(z) (¦'(z)-1)^
= v(z) (¦-1'(Z))^
.
The Joukowski transformation Z = ¦(z) = (z-d)+f2(z-d)-1
with dZ/dz = 1 - f2(z-d)-2 ;
(d/dz)2Z = 2f2(z-d)-3;
and
bivalued inverse
z = ¦-1(Z) = ½(Z ± (Z2-4f2)½) + d .
We frequently take real f2=f2 real and d=0.
¦ maps z=d±f to Z=±2f and circles to a general "aerofoil like"
family of 2D 1-curves including ellipses and ridged teardrop shapes.
To make ¦-1(Z) single valued, we choose the square root q=(Z2-4f2)½
"nearest" to Z in that q^*Z ³ 0 and refer to
¦-1+(Z) = ½(Z+q) + d acting like a d displacement for large r
as the principle Joukowski inverse ; and to
¦-1-(Z)=½(Z-q) + d = f2(¦-1+(Z)-d)-1 + d
acting like f2Z-1 + d
= f2|Z|+-2 Z^ + d
for large Z as the secondary Joukowski inverse.
There are discontinuities in ¦-1+ and ¦-1- along the line segment connecting
Z = ± 2f acrioss which ¦-1+ and ¦-1- "switch values".
A Joukowski aerofoil is the image under ¦ of a circle |z-c|+=a, usually one containing
d-f inside it and c+f either inside the circle or on it.
Havning d+f on the circle requires c = d+f + a(ig)↑
and |d-f-c|+ £ a
whence cos(p+g-z) ³ a-1f where f=f(iz)↑.
A Joukowski aerofoil has boundary
|¦-1(Z)-c|+ = a but there is a difficulty knowing
which inverse to use. If c lies on the line connecting d±f then the aerofoil
is symmetric and convex and is all "carried" back from Z space
to z space by ¦-1+. But if c lies sufficiently far from the
the d±f connecting centre line, part of the boundary is concave and the region between this and the centre line
is carried by ¦-1- .
The actual condition for the interior of the aerofoil is
|¦-1+(Z)-c|+ £ a
&
|¦-1-(Z)-c|+ £ a
and we can move the discontinuity from the centre line portion exterior to the aerofoil to the boundary of the aerofoil
by switching to ¦-1+ when |¦-1-(Z)-c|+ £ a .
¦-1±'(Z) = ½(1 ± q-1Z)
and ¦-1±"(Z) = ±½q-1(1 - q-2Z2)
so ¦-1+'(Z)+¦-1-'(Z)=1 and
¦-1+"(Z)+¦-1-"(Z)=0 .
Â2 Flow Past a sharp edged 2D Boundary
Joukowski-Kutta Condition
The Joukowski warped flow velocity V(Z) = v(z) (1-f2(z-d)-2)-1^
is infinite only when v(z) is or when (z-d)2 = f2 with z lieing outide the boundary
and v(z) nonzero. Thus if one of z=d±f lies outside
a given closed y(z) streamline conisdered to be a boundary,
then
only by choosing the circulation G to ensure a stagnation
point f'(z)=0
at that z can we eliminate an aphysicsl point of infinite flow.
For a generalised circular flow
f(z) = a(z-c) + a2a^(z-c)-1 + G(z-c)↓
with f'(z) = a - a2a^(z-c)-2 + G(z-c)-1
finite everywhere but at z=c
we have stagnation whenever
a(z-c)2 + G(z-c) - a2a^ = 0 which
at z=d±f
requires G =
(d-c±f)-1
(-a(d-c±f)2 + a2a^) .
If z=d-f lies within our z space boundary streamline and z=d+f lies on it
with c = d+f + a(ig)↑ then for real a=a we have purely imaginary
G = (-a(ig)↑)-1
(-a(-a(ig)↑)2 + a2a^)
= -a(-a(ig)↑) + a^(-ig)↑))
= 2aA sin(g-a)i
and hence G = -4paA sin(g-a) .
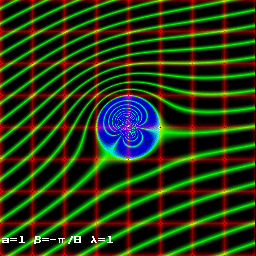
For a symmetric aerofoil with g=p we have G=-4paA sin(a) .
| Joukowski-Kutta condition flow around a Joukowski aerofoil .
|
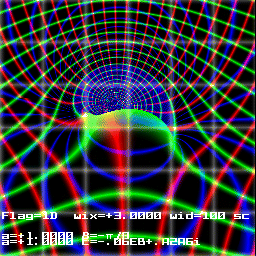
Principle flow F+(Z)
| 
Reciprocal flow F-(Z)
|
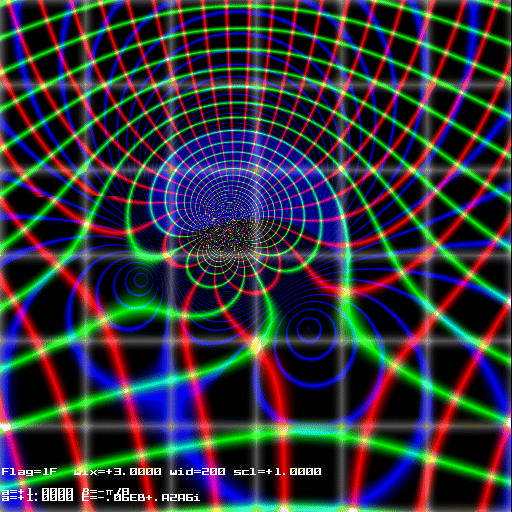
Summed flow F+(Z) + F-(Z)
|
|
yp streamlines in green; fp isopotential lines in red; |Vp| isospeed lines in blue.
|
If one or both of
d±f lie on a boundary C in z space then the warped boundary ¦(C)
in Z space has a gradient discontinuity
at ±2f since
f'(z) = ½(1 - f2z-2) vanishes at z=±f but
f"(z) = f2z-3 is ±f-1 there .
The reciprocal Joukowski inverse
¦-1-(Z)=½(Z-q) + d = f2(¦-1+(Z)-c)-1 + d
has |¦-1-(Z)-d|+ = |f2|+|¦-1+(z)-d|+-1
[ Proof :
¦-1-(Z)-d|+2 =
(f2(¦-1+(Z)-d)-1)^
(f2(¦-1+(Z)-d)-1)
= |f2|+2 |¦-1+(z)-d|+-2
.]
Consider a d=0 Joukowski warp Z = ¦(z) = z+f2z-1 acting on a circle of
centre c=lf
and radius a=(1-l)f chosen so that the circle
passes through z=f and z=(2l-1)f
and also z=(l±(1-l)i)f
while the Joukowski aerofoil passes
through Z=2f and
Z = (2l-1)+(2l-1)-1)f
and Z=(l±(1-l)i + (l±(1-l)i)-1)f
= (2l±2l(1-l2)(l2+(1-l)2)-1i)f.
Taking l<0 encloses -f inside the circle and we are left with a boundary gradient discontinuity
with stagnation there if G = -4paA sin(a) =
-4pf(1-l)A sin(a) .
The symmetric aerofoil has length L
= (2-(2l-1)-(2l-1)-1)f
= (3-2l+(1-2l)-1)f
and width W=4l(1-l2)(l2+(1-l)2)-1f.
Small negative l yields a thin aerofoil
with L=4(1+l2+2l3+...)f » 4f » 4a
and W » lf with
critical circulation
G=-4paA sin(a) » -pAL sin(a) giving lift
F » 4praA2 sin(a) ((a+½p)i)↑
. Letting l®0 gives a flat plate of exact length L=4a and
critical circulation G=-pLA sin(a).
Large negative l yields a "dimpled circular" aerofoil with L » W » 2lf » 2a
and critical circulation G=-2pLA sin(a).
These results appear bizarre, with the sin(a) factor suggesting lift is maximised for an aerofoil moving perpendicularly against the flow,
and the dimpled circle of a diameter L twice as efficient at generating lift as a flat plate of length L.
In practice, the dragless circular flow fails
for attack angles exceeding about 20 o or nonthin aerofoils, with seperation of the flow from the aerofoil surface
and turbulance in the wake rather than a smooth "reclosing" of the flow behind the aerofoil resulting
in the lift for increasing a, a pheneomena known as stalling.
At the stalling angle, the airflow typically "seperates" from the upper surface and forms unsteady turbulence and eddies. Some authors refer to
stalling as the point where lift becomes negative, but this is erroneous.
Stalling occurs when the still positive lift begins to decrease with increasing attack angle.
For small attack angles the sin(a) factor holds
resulting in lift being roughly linear in a until the stalling angle is approached.
Deriving the critical
Kutta-Joukowski circulation and hence the lift for a general sharp-edged aerofoil
is problematic and various iterative methods such as that of Theodorson have been developed.
Aerofoil Waffle
Loosely speaking, if a is well inside [-½p,+½p] so that the flow is approximately horizontal left to right, and the circulation is negative (clockwise) then
the flow is slower beneath the aerofoil than above it so the pressure s0-½rpVp2
is greater below the aeorfoil than above it and the lift force exerted on the airofoil is vertically upwards
and this is the force that holds up an aircraft. In practice the decrease in pressure above the wing is usually gretaer than the increase in pressure below it
with up to 80% of the lift stemming from "pulling" of the upper surface wing rather than "pushing" of the lower.
Both changes are greater near the leading edge of the wing so that the net torque on the wings serves to
raise the leading edge and we can think of the centre of pressure - being the point on a
designated aerofoil chord line through which we must consider the lift force to act if its couple about the aerofoil centre of mass is to match
the picthing moment - as moving forward. The picthing moment exerted in the wings is typically balanced by the upward lift on horizontal tail fins.
If we lower (or raise) a flap at the trailing edge of an airfoil we will increase drag and slow the
fluid flow below (or above) the airfoil, resulting in an increase (or decrease) in lift.
Thick airfoils, convex or concave, present the problem of lacking a single unambiguous "forward" direction
with reference to which one can define an "attack angle".
The chord line of a (planar section of) an airfoil is the line joining the leading edge
to the tailing edge is sometimes used.
Lift Proportionate to v2
Suppose S is a small planar element
of area content s having unit normal n, and centre of mass c travelling with constant velocity v through a fluid of density r initially
at rest. Assume n is signed so that n¿v ³ 0 .
In small time dt the simplex must displace a small volume s(v~¿n)|v|dt
= s(v¿n)dt
which we assume to act as a single impactive mass we can consider as having
velocity -v and momentum
= rs(v¿n)vdt
on an unmoving simplex.
If the impactive impulse T parallel to n is sufficient to precisely eliminate the n component of the velocity
so that the displaced air "slides off" the simplex we have
T =
rs(v¿n)dt (v¿n)
= rs(v¿n)2dt
which is percived by the simplex as a "drag impulse"
- rs(v¿n)2dt (v~¿n) parallel to v and a "deflective impulse"
- rs(v¿n)2dt (1-(v~¿n)2)½
- rs(v¿n)2dt cos(a) where a = ½p - cos-1()(v~¿n)
is known as the angle of attack in the context of a thin planar airfoil.
This is a gross simplification of airfoil dynamics but substantiates somewhat
our assertion that the forces acting
on an airfoil are roughly proportionate to the square of the airspeed as well as to the area of
the "leading" surface.
Force Velocity Coefficients
Broadly speaking (and for subsonic speeds), the lift and drag are individually proportional to v2 , the density of the medium, and the
(XY planar) area of the airfoil and this is usually expressed for N0=3 as
L = ½rSv2 CL,a,b ;
D = ½rSv2 CD,a,b ;
C = ½rSv2 CC,a,b
where r is airdensity, S is wing area and CL,a,b, CD,a,b
, CC,a,b
are known as lift coefficient , drag coefficent, and crosswind coefficient
for attack angle a=q-½p and yaw angle b=f for the airfoil orientated with e3 upwards
amd e1 forward. These are the projections of T into the wind frame , with D parallel to v ,
L lieing along ¯v*(e3Q) , and (moving to 3D) C perpendicular to both.
For a (Z) symmetric airfoil , CL,0,0 = 0 while CD,0,0 ³ 0 since v is here the velocity of the fluid past the aerofoil rather than the velocity of the aerofoil trhough the fluid. Modern airfoils are asymmetrically cambered to give
small CL,0,0 > 0. The crosswind force is frequently neglected, or assumed cancelled by the opposing crosswind force on a symmetricaslly
opposing aerofoil.
For inviscid irrotational steady flow we have
CD,a,b=0 ; CL,a+p,b= CL,a,b ;
CC,a+p,b=- CC,a,b but in practice we usually have
aerofoils less efficient when travelling backwards with
CD,a+p,b > CD,a,b > 0 and CL,a+p,b £ CL,a,b
Aerofoils are frequently characterised by providing CL,a º CL,a,0,
CD,a, and CM,a, for a limited range of a typical in
normal flight, say -4 to 20 degrees
though the values
RD L(a)=
( CL,a2+ CD,a2)½
and QD L(a)= tan-1( CL,a/ CD,a)
are arguably more "natural"
since for N0=2 we have
F
= ½rSv2RD L(a)(QD Le21)↑v~
= ½rS|v|RD L(a)(QD Le21)↑v
with
QD L(a)=±½p for dragless lift.
Sometimes CD,a=(pEA)-1 CL,a2 is assumed where efficiency E»1
and A is a aspect ratio.
For aerobatic emulation purposes we typically require values for all a and b.
For large a the aerofoil can sometimes
be considered a flat plate, although as the dragless circulatory flow model fails for large a for flat
plates an alternate high drag model model should be employed.
CL,a is small or zero for zero a, rising roughly linearly to a maximum
at a stalling angle of about 16 degrees, and then falling off in an uncertain manner,
possibly to zero value and zero gradient at ½p.
For aÎ(½p,p]
we might crudely assume
CL,a+p=mL CL,a where 0<mL£1 is a reversal inefficiency factor.
and characterise or tabulate CL,a only over [-½p,½p) .
The assumption that the reversal lift profile has the same shape as the forward one is unrealistic but if we expect
an aerofoil to seldom travel backwards it may be acceptable.
For aerofoils symmetric in their e1W chordline, the lift for attack angle -a is minus that due to attack angle a.
One possible strategy is to assume that for b Î [0,½p]
CL,a,±b = cos(b)2 CL,a,0+ sin(b)2 CL,a,±½p and tabulate forwards and sideways
lift coefficients
CL,a,0 and CL,a,±½p over aÎ[-½p,½p) , with CD,a,b,
CD,a,b and the moment coefficients implemented similarly.
The use of cos(b)2 and sin(b)2 weights ensures that CL,a,b= CL,a,0 for a
solid of revelution about e3W
disk like aerofoil.
Sometimes one or more of the ½, r and S
are amalgamated into the coefficients ,
although r does decrease with altitude and varies across shock waves. However, keeping the density r and area S outside the coffecicients
keeps them dimensionless, dependant only on the shape rather than the size of the aerofoil.
Torque Velocity Coefficients
The point of a 2D airfoil through which the lift and drag forces can be considered as acting (for a given a),
known as the centre of pressure is also relevant, for unless this happens
to be the centre of mass of the airfoil, the forces will indice a torque known as a pitching moment tending to rotate the airfoil.
This torque is often written as ½rScv2 CM,ap) where CM,ap) is the pitching moment coefficient
for attack angle a and point p, about which the torque is computed. c is the chord length.
We will again embody the ½rS and now c also into the coefficient and obtain
hp = v2 CM(a,p) for the picthing moment about a Y-eaxis through point p.
For many airfoils there is a point a (more accurately an axis) known as
the aerodynamic centre about which the pitching moment for a given airspeed v2 is largely invarient with a
(at least over a typical flight range of a of -8 to 16 degrees) so that the moment coefficient CM,aa) is independant of a.
This point is usally about ¼ chordlength back from the leading edge of the airfoil, and the constant torque tends
to be signed so as to lower the lower nose and raise the tail of an aircraft (or twist the wings from the fuselage!)
The pitching moment tending to rotate the aerofoil is usually taken to be
½rVp2ScCm(a,b) where c is a mean chord length
and Cm(a,b) is a dimensionless coefficient.
Similarly for a 3D aerofoil we have rolling and yawing torques about the v~ "wind upward"
axies exerted on the aerleron due to the fluid drift v.
Bimpulses due to spin
Even under our assumption that the fluid velocity is uniform in the vicinity of the body, a nonzero
spin w of the body means that the fluid encountered by the body surface will have varying relative velocity.
If an aircraft is rolling anticlockwise about e1Q so that its left wing is rising, for example, then
the effective angle of attack a of the airstream over the left wing is decreased at a point l out along the wing
by roughly lw23|v|-1
while that on the right wing is increased by about the same ammount.
Assuming that all the lift ½rv2CL derives from the wings, these
changes in a result in lift decreasing and increasing by
½r_dlcv2 lw23|v|-1 ¶CL/¶a
on the left and right wings respectively, imparting a clockwise torque
r|v_dlcl2w23¶CL/¶a
acting in conjunction with and probably exceeding any "fractional" torque proportionate to
(w23)2
opposing the roll.
We can regard this as providing an addition
½l|v|-1w23¶CL/¶a to the roll coefficient
C23(v~)
= C23(a,b) providing the characteristic length l used for the effective wing length
is the same as the length used to render the roll coefficient dimensionless.
Similarly, an anticlockwise yaw about e3Q bringing the right wing forwards will,
if the aircraft is travelling horizontally with nose slightly raised, tend to decrease the right wing attack angle but increase its effective speed
causing a net increase in lift on the right wing and a decrease on the left, resulting in a torque inducing a roll
lowering the wing on the "inside" of the yaw. This can be crudely modelled by a further addition
½l|v|-1w12¶CL/¶b to the roll coefficient
and in general we model the biimpulses due to spin by adding such terms involving a and b derivatives of the velocity based force
coeefficients to the ½N0(N0+1) velocity response coefficients.
Consider a long wide aerofoil of stance 1 travelling with
velocity v=(-ae31)↑e1 » e1-ae3 for small a and spinning
at w. A segment at le2 has velocity v+le2Ùw.
Let us first consider yaw rotatiaon with w=we12 with w>0. The segment velocity is then_v-lwe1
so for l>0 the speed decreases but the attack angle increases unless a=0.
Matters thus simplify if a=0 since then the attack angle remans constant and the speed becomes
v-lw so that the total lift is
F = ò-LL dl½rc(v-lw)2 CL,0 e3
= ½rS CL,0(v2 + 6-1(2L)2w2)e3
where L is the demiwingspan and c=(2L)-1S approximates the chord length for a thin aeorfoil.
The total roll torque is
ò-LL dl½rcl(v-lw)2 CL,0 e23
= -12-1rS CL,0v(2L)2we23
equivalent to adding -6-1 CL,0v-12Lw to the velocity based roll moment coefficient.
For nonzero a but zero b we have
sin(Da)(lw)-1 = sina(v+Dv)-1
F = ò-LL dl
½rc((v cos(a)-lw)2+v2 sin(a)2)
CL, tan-1( sin(a)( cos(a)-v-1lw)-1) , typically
with |lw|<<v .
This is the model used by many flight simulators. The six (½N0(N0+1) for N0=3) velocity induced wind frame force and torque coefficients
for the whole aircraft are tabulated, often with thousands of data points perhaps
clustered more densely over more common regions , over the encountered ranges
of flight (wind) angles a,b and mach speed M.
Effects due to aircraft spin, acceleration, propellor thrust, flap settings and so forth are
the implimented as approximations based on the velocity coefficients such as the addition of
½lw23|v|-1 ¶CL/¶a
to the roll moment velocity coefficient, obtainable via a calculated differential of the tabulated CL,a,bM) surface.
It is hard to adapt this whole-body model to accomodate damage to particular regions. If a rear tail fin is half shot off, for example,
then we lack LUTs for the new assymetric composite aircraft.
For the emulation of near level flight when velocity is largely forward with speed sufficient for the lift to roughly balance the gravitational weight we can
safely extract the Vp2 and parameterise the coefficients solely by airspeed direction but for acrobatic flights
involving high spins and accelerations our coeffecients become functions of w as well as v
and any control parameters.
We can extend our
½N0(N0+1) boy frame coefficients as
T = ½r|W|2Såi<jli
Cij(W~,m,M)eij¥
where W is the bivelocity of magnitude |W| and M is the mach speed of v.
The advantage of moving the v2 outside the velocity coefficients where twofold. First, it makes the coefficient
dimensionless, and second it makes it a function of only the direction v~. This second advantage is voided if the mach speed M
is reintroduced as a parameter so we may as well declare
T = ½r|W|2Såi<jli
Cij(W,m)eij¥ with dimensionless coefficients that are functions of the unnormalised ½N0(N0+1) coordinate bivector W
and a control vector m.
Propellers
The principle example of a nonfixed aerofoil subbody is a propellor blade. These will typically be mounted at symmetrically
on an aircraft with e3P = e1Q and be spun rapidly about this axis by an engine
to provide a forward thrust usually adequate only for subsonic flight, or lift in the case of a helicopter.
The path taken by a point on the propellor is a helix, skew if vPQ ¹ e1
and curved if wQ¹0.
The instantaneous force exerted on the propellor
has a "thrust" component along e1_APlane and a "torque" conmpoent perpendicur to it
which is typically balanced by and opposite torques from
the opposite arm of a two-blade propellor, or averages out over a propellor rotation.
The net force exerted on the propellor centre is typically parallel to e1_APlane but induces a troque on the aircraft if the
propellor centre cPQ lies off the centre line of the aircraft. Propellors are typically symmetrically or centrally mounted
but may be above or below the aircraft mass centre and so impart a pitching moment.
Propellors accelerate the air passing "through" them and typically increase the airspeed over the wings and/or tail and hence lift.
They also act as gyroscopes resisting pitch and yaw torques.
Consider a point at -ye2 of a propellor having stance 1 and bivelocity
W=(1+½v_e3e)w_e12_frm2(P,Q).
Its velocity is ywe1+ve3 which we can regard as a 2D areofoil travelling at speed
(y2w2+v2)½ with attack angle g(y)-q(y)
where angle g(y) is the pitch of the propellor blade at distance y from its hub
and q(y)= tan-1(v(yw)-1). The force along e3 acting on the 2D section
is
dF =
½rdS(y)(y2w2+v2)(
CL(g(y)-q(y)) cos(q(y)
-CD(g(y)-q(y)) sin(q(y))
=
½rdS(y)
RD L(g(y)-q(y)) sin
(g(y)-q(y)) cos(q(y)
- QD L(g(y)-q(y)) )
where dS(y)=dy L(y) is the propellor area element. Integrating this over y from 0 to the propellor span
gives the instantaneous forward (e3) force exerted by one blade of the propellor.
However, and easier way to estiamte the total force T=Te3 exerted by a propellor on its mounting point
is to assume that the propollor has a given efficiency EÎ[0,1] so that
if the engine exerts a torque Q and so does Qw work then EQw = T_vu3
where _vu3 is the forward speed of the aircraft, so that T=(_vu3)-1Qw.
Body Frame Coefficients
Returning briefly to 2D, our notion of fluid drift v=A(ai)↑e1
travelling for small attack angle a from left to right suggests an aerofoil W aligned with its forward direction e1W=-e1 facing right to left.
More generally, we might expect an aircraft Q to be pointing roughly into the enocuntered windpeed with v~ » -e1Q .
If we wish to work in the frame of the aerofoil it is sensibkle to take v to be negative the encountered fluide velocity
so that directly forward motion of the aireofoil corresponds to a=b=0
More generally we can define
N0+½N0(N0-1)=½N0(N0+1) dimensionless coefficients defined by
expressing the 3-vector bimpulse
T = ½rv2Såi<jli
Cij(v~)eij¥
in the frame of the body rather than the windframe. Here i,j are from {0,1,..,N0} , li is a characteristic length of the aerofoil in the i dimension with
l0=1, and
Cij(v~) is a dimensionless scalar coefficient.
C01(v~) is the forward coefficient with
C01(p-a,0) = - cos(a) CD,a,0+ sin(a) CL,a,0 ;
C02(v~) is the sideways coefficient ;
C03(v~) the upward coefficiecnt with
C03(p-a,0) =
cos(a) CL,a,0+ sin(a) CD,a,0 ;
C13(v~) the body pitching coefficient
with C13(p-a,0)= CM,a,0
, and so on.
In 3D we can approximate these using
Cij(a,±b)
= cos(b)2Cij(a,0) + sin(b)2Cij(a,±½p) as for the windframe coefficients
and because we are now measuring the coefficients in the body frame, for sideways symmetric 3D
body symmetric in y=0 we have
Cij(a,-b)=±Cij(a,b) with the - occuring when one of i or j is 2.
Speed of Sound
Compressable fluids can carry density waves
Even though in theory the velocity based flight coefficients depend only on the direction Vp~ and not on the magnitude Vp2, in practice they do vary with the speed
partcularly when distingusihing slow, subsonic, and supersonic flight.
It is natural to express the airspeed |v| as a fraction of the speed of sound s=(r-1m)½
where fluid stiffness coefficient m has units kg m-1 s-2, ie. we set
|v| = M(r-1m)½ for unitless mach number or mach speed M so that dymanic pressure
½rv2 = ½M2m is independant of the density r; or rather
its dependance on r is subsumed into M
. For M>1 we have supersonic speed
and M>5 as hypersonic speed .
The speed of sound varies with density and tempreature and the nature of the fluid but for air at sea level
it is roughly 28.4 ms-1
Furthermore, aircraft typically have control surfaces like aerlerons and flaps whose orientations are varied to
effectively alter the flight coefficients of the wings or fins to which they are attached.
The settings of such control surfaces are typically parameterised by angles and we have a
control vector m fromed from these angles.
Body as rigid amalgamation of simpler subbodies
An aletrnative approach is to consider the aircraft as composed of a collection of rigidly connected aerofoils, each with their own aerodynamical coefficients.
We might for example consider the left wing to be composed of one or more wingsections.
Assuming a particular wing section W to be at rest with respect to the aircraft, the instantaneous apparent bivelocity of the fluid as percieved by W is
-WWW =
-RW4§§(cQ4dt)e¥
- RWQ§(
(cWQ¿wQQ )e¥
+ wQQ
)RWQ
and we can use this to construct the biimpulse about the W centre
TW(-WWW)
applied to the wing section in the frame of the wing section and then recast this as
RWQ§( TW(-WWW) ) into biimpulse about
cWQ applied to the aircraft,
assuming the imulses and tiorques involved are inadequate to deform or dislodge the wing section.
The biimpulse about the aircraft centre in the aircraft frame is
RWQ§( TW(-WWW) )
+ cWQÙ(
e¥0¿
RWQ§( TW(-WWW) ) )Ùe¥ and by adding
such centred biimpulses for all the aircraft subbodies we obtain a net biimpulse Tc acting on the aircraft
about its centre c which we typically take to be be the mass centre.
The kinematical responce of the aircraft is then given by
DW = H-1Q(Tc).
This method is again highly artificial. Even in steady, level flight, the airflow encountered by
tail is typically in the downward deflected downwash from the wings, and so has its attack angle lessened.
In accelerative motion, vortices or similar flow effects shed from the wings hit the tail planes after a delay roughly proprtionate to
|v|-1, a crosswind coming from the left is partially screened from the rightwing by the fuselage,
and in general the fluid flow in the vicinity of the body is extremely complicated. However, modelling the fluid itself
is typically computationally out of the question and the best we can hope for is broadly plausable behaviour
of the body moving through it.
Leftovers
Problems with 1-flows
Imagine a medium consiting of two types of particle. "Green" particles of small unit "mass" and unit positive "charge",
and "red" particles of unit mass and negative charge which
with regard to a partcular observer e4 , are confined to a ring of radius R centred on the origin,.
Assume that there are equal large quantities of green and red particles
distributed with uniform density r particles per (small) unit volume around the ring
and that particles contrive to avoid impacting eachother, or do so only rarely. Assume
that the green partciles are travelling "anticlockwise" around
the ring with orbital period T while the red particles travel clockwise with the same orbital period.
The net spacial flow of mass through a given cross sectional ring element is then Mp=0,
although there is kinetic energy
2r½(2pR/T)2 = r(2pR/T)2 .
The net spacial current flow is 2 r(2pR/T) anticlockwise . If the red particles were all to reverse direction, and flow counterclockwise,
we would have zero current
but nonzero momentum.
This simple example demonstrates the complications in "adding up" flows. Allowing negative and postive charges
means that the sum of two charge-weighted timelike vectors may not remain timelike.
Generally speaking, when adding four-momentum 1-vectors, relative masses combine additively but
relative three-momentum magnitudes incurr a triangle inequality so that proper magnitude is not conseerved
and tends to increase .
When physicists speak of the flow "at" a particular point they usually mean the averaged flow over a small volume at that point, and by "small"
they usually actually mean large enough to contain multiple particles. They hope by summing a large
number of fundamentally discontinous point-dependant "path localised" functions to produce a continuos field.
Thus all the matter at a given event p is considered to be effectively flowing with the same direction and speed.
We will refer to such a flow as single flow because all the matter at p is effectively doing the same thing.
More generally we represent a superposition of 1-flows with a 2-tensor vp such that
vp(l,d)aÙb provides the number of particles of the matter at p of
kind classified by a matter-type indicator l
flowing across spacial 2-plane aÙb in e4-time d. By which we mean
that on fixing any timelike e4 perpendicular to a and b the integer number of particles crossing
between e4-times t and t+d divided by d.
In the sense of vp representing the documentation of an actual multiparticle flow,
we regard vp(l,d)aÙb to be valued in integer multipes of d-1
rather than a full real type.
As d®0 the integer multipliers get smaller discontinuously.
If the flow is steady in the sense that at a suffiicently small d the second derivatives
become swamped by the first and we can conceptually replace individual particles with
shoals of identical smaller particles having parallel trajectory
then we expect vp(l,d)aÙb to approach a limit .
Flow is thus more naturally regarded as a bivector which we will call 2-flow. For N=3, the 2-flow is dual to the 1-flow .
Flow rond moving sphere
Bernouilli's equation concerns a sphere moving through a fluid and states that at anypoint near the surface of a frictionless
sphere whose centre moves with low velocity v Î e12 in the x3=0 plane is
sg-1 + x3 + ½v2g-1 = k
where s is the fluid pressure , g is gravitational accelaration, and k is a constant.
Thus there is a symmetry to the flow and the fluid is left essentially undisturbed, no energy is lost,
and drag is zero.
If the velocity, or friction, increases, there can instead be eddies or turbulance in the "wake" of the sphere.
imparting energy to the fluid and so slowing the sphere;s travell.
In practice the "impactive drag" or form drag on a sphere is about half that on a flat plane of
identical leading area travelling
"flat on" (a=½p , v~=n) . Optimal streamlining can reduce this drag to about 5%.
We can rearrange Bernoulli as
sr-1 + ½v2 + x3g = kg and if the sphere is small so that
x3g may be neglected we have
s + ½rv2 = kgr . If the fluid is considered as incompressible
so that r is constant we refer to constant s0 º kgr
as that stagnation pressure since it correspends to P when v=0,
and ½rv2 = s<0>-s as the dynamic pressure.
Hence the greater |v|, the less s , provided |v| remains small enough (less than half sonic speed)
for the Bernouilli equation to approximately hold .
 Extremal M-Curves
Extremal M-Curves
A standard problem in classical mechanics is to determine the form of the curve assumed by a
rope of length a hanging motionless between two fixed points a distance less than a apart
under a uniform gravitational field, which is an extremal 1-curve in N=2 dimensions.
If we assume the rope to hold a curve shape p(s)=(x(s),y(x))
(the Y axis being gravitationally vertical) that does not loop "over" itself vertically, we have
'2 = dx2 + dy2 so that the length constraint is
a = ò01 ds = òx0x1 dx(1+y'2)½
where y' º dy/dx.
The mechanical constraint is that total gravitational potential energy
ò01 ds rgy(s) = rg òx0x1 dx y(1+y'2)½
be minimised,
where g is uniform vertical gravitational acceleration and r is the mass of unit length of rope.
More generally, we might seek to minimise
òx0x1 dx¦(x,y,y') subject to a constraint
òx0x1 dxg(x,y,y') = a.
A standard approach is to form h(x,y,y') º ¦(x,y,y') + lg(x,y,y')
where scalar l is known as a Lagrange multiplier. One then embodies freedom to vary the
path by means of two
z0 and z1 such that
y(x0,z0,z1)=y(x0) ; y(x1,z0,z1)=y(x1) " z0,z1 (boundary condition)
; y(x,0,0)=y(x) ; and y(x,z0,z1) is twice continuosuly differentiable in all parameters.
Forming K(z0,z1) = ò+x0x1 dx h(x,y(x,z0,z1),y'(x,z0,z1)) the extremal condition requires
¶K/¶z0 and ¶K/¶z1 to vanish at z0=z1=0 and this leads (via integration by parts)
to the Euler-Lagrange equation
¶h/¶y = d/dx(¶h/¶y') .
In the case of the hanging rope,
h(x,y,y') = (rgy-l)(1+y'2)½ and setting l = -rgy0 we have
h(x,y,y') = rg(y-y0)(1+y'2)½
= rg(y-y0)(1+(y-y0)'2)½ for some constant y0 .
Setting h = y-y0 the Euler-Lagrange equation is
rg(1+h'2)½ =
d/dx rghh'(1+h'2)-½
with first order simplification
h' rghh'(1+(y-y0)'2)-½ -
rgh(1+h'2)½ = b
Þ
rg(1+h'2)-½h = b
having solution h = b cosh(x-c)/b) so the rope has shape
y0 + b cosh((x-c)/b) where c,y0 and b are chosen to
match the given endpoints.
We say an M-curve CM is M-extremal for an action functional
¦CM:UN ® UN if some particular magnitude measure (content, scalar part, square, modulus or whatever) of
òCM dM-1p ¦CM(p) is maximised (or minimised) by CM in the sense that
integrating other any M-curve which deviates only slightly from CM will produce
a result no higher (or lower) than the CM integral. CM is a "locally optimal"
M-curve for a particular integration ¦CM. We specify the dependancy of ¦ on CM to allow
action functionals dependant on the geometric properties of the "sampling curve" CM , such as tangent
or normal vectors , to allow "direction dependant sampling" or "velocity dependance".
Euler-Lagrange Equations
For M=1 we have a path p(s) 1-extremal for FC1 = F(s,p(s),p'(s)).
Hamilton's principle provides that the state of a system characterised at time t by k multivector variables
x1(t),..,xk(t) varies from time t0 to t0 so as to 1-extremise
a (usually real scalar) integral measure
S(t) º S(t0) + òt0t0 dt L(t,x1(t),..,xk(t),xdt(t),...,xkdt(t))
with the action functional L(t,x1(t),..,x1dt(t)) known as the Lagrangian
of the system.
L is usually assumed to be real-scalar valued and independant of p"(t) and higher derivatives and is
traditionally assumed to seperate into "kinetic" and "potential" componenets independent of time and velocity respectively
as
L(t,p(t),p'(t)) = T(p(t),p'(t)) - V(t,p(t)) but more generally we might postulate
a multivector-valued Lagrangian of k multivector-valued variables and their first temporal derivatives
L(t,x1(t),..,xk(t),x1dt(t),..,xkdt(t)).
If the Lagrangian L is itself an integral over some spacial M-curve (typically an
M=N-1 hypercurve reprenting a contemporal slice of a Base space)
L = òBase(t) dN-1p L(t,p,pdt)
that spacially integrated function is known as a Lagrangian density. Note that such requires a "velocity" pdt be associated with every point p in Base(t) .
Extremal Paths
A standard approach for M=N=1 to 1-extremise ¦(s,x,x')
is to embody freedom to vary the path by means of two scalar parameters
z0 and z1 such that
x(s0,z0,z1)=x(s0) ; x(s1,z0,z1)=x(s1) " z0,z1 (boundary condition)
; x(s,0,0)=x(s) ; and x(s,z0,z1) is twice continuosuly differentiable in all parameters.
Forming K(z0,z1) = òs0s1 ds¦(s,x(s,z0,z1),x'(s,z0,z1)) the extremal
condition requires
¶K/¶z0 and ¶K/¶z1 to vanish at z0=z1=0 and this leads (via integration by parts)
to the Euler-Lagrange equation
¶¦/¶x = (d/ds)(¶¦/¶x') .
In particular cases where ¦(s,x,x') = ¦(x,x') so that ¶¦/¶s=0 and there is no explicit s
dependence,
we have d/ds(x'¶¦/¶x' - ¦)= 0
giving a first order differential equation
x'¶¦/¶x' - h = constant .
[ Proof : y" ¶h/¶y' + y'd/dx¶h/¶y' - ¶h/¶x-¶h/¶yy' - ¶h/¶y'y"
= y'(d/dx¶h/¶y' - ¶h/¶y) - ¶h/¶x
= 0
.]
A nongeometric generalisation is to extremise òs0s1 ds¦(s,x1,x2,..xk,x1',x2',..xk')
subject to M scalar constraints gi(s,x1,x2,...xk)=0 i=1,2,..,M
(Note the absence of any g dependance on the xi').
To do so we form
h(s,x1,..,_xK,x1',..,xk') = ¦(s,x1,..,_xK,x1',..,xk')
+ åj=1M lj(s)gj(s,x1,..,xk,x1',..,xk')
where lj(s) are M arbitary functions of s
and obtain Euler-Lagrange formulae
¶h/¶xi = (d/ds)(¶h/¶xi') for i=1,2,..k .
Generalising geometrically, we have F(s,x1,x2,..,xk,x1',x2',..,+xk')
with geometric Euler-Lagrange Equations
¶F/¶xi = (d/ds)(¶F/¶xi') " i=1,2,..k
and first order equation
åi=1k (xi'*Ñxi')F - F = constant (independant of s)
if ¶F/¶s = 0.
Considering the xi as seperate grades of a single multivector argument x we can regard the Euler-Lagrange equations
as individual coordinate terms of a single geometric equation
¶xF(s,x,x') = (d/ds)(¶x'F(s,x,x'))
where ¶x = åijk.. eijk..¶/¶xijk..
over all blades comprising x space so that, for example,
¶x = åi=1N ei(¶/¶xi).
Generalised Momentum
When F is a scalar-valued Lagrangian we have (xi'*¶xi')L =
xi'*(¶xi'L) and multivector m = Ñxi'L(x1,..xk,x1',..,xk)
is known as generalised spacial momenta or cononical momenta.
Typically xi' is spacial 1-vector valued and so momenutum is a spacial 1-vector.
If multivector L is independant of xi so that ¶L/¶xi=0 then the ith Euler-Lagrange equation provides
(d/dt) ¶L/¶xi' = 0 so Mi = ¶L/¶xi' is constant, ie. unchanging with t,
Thus the constants of a system are consequences of absent dependendencies (aka. symmetries) in the Lagrangian.
Energy is conserved when L depends on t only indirectly via x(t) and it derivatives.
Momentum is conserved when L depends on x only indirectly via x'.
For L(t,x,x') = ½mx'2 - f(x,t) we obtain classical momentum
Ñx'½mx'2 = mx' , constant if f(x,t)=f(t).
Adding an electromagnetic term qc-1ax¿x' to L introduces
qc-1ax to the momentum
If
L(t,x1(t),..,xk(t),x1dt(t),..,xkdt(t))
= L(x1(t),..,xk(t),x1dt(t),..,xkdt(t))
so that there is no explicit t dependance then
the Hamiltonian H(x1(t),..,xk(t),x1dt(t),..,xkdt(t))
º åi=1k (xidt*Ñxidt)L - L is a constant,
the "energy" of the system.
We can regard the Hamiltonian as generalised temporal momentum. Conservation of energy but varying spacial momentum
resulting from only non-relativistic potentials f(x,t)=f(x) .
But H = - ¶S/¶t .
Even though, like the Lagrangian, S(t) cannot strictly be regarded as a function of position since it is only defined over
our given extremal path, we can nontheless postualte an action field S(t,x) an it can be shown that
m = (xi'*¶xi')L = ÑxiS(t,xi) and in particular we have the Hamilton-Jacobi equation
H(xi,xi',t) = -¶S/¶t
[ Proof : For any ¦(x,x')
d/dt ( åj=1k xi' ¶¦/¶xj' - ¦)
= åj=1k xj" ¶¦/¶xj'
+ åi=1k xj' d/dt ¶¦/¶xj'
- ¶¦/¶t
- åj=1k ¶¦/¶xjxj'
- åj=1k ¶¦/¶xj'xj"
=
åj=1k xj' d/dt ¶¦/¶xj'
- ¶¦/¶t
- åj=1k ¶¦/¶xjxj'
=
åj=1k xi'( d/dt(¶¦/¶xj') - ¶¦/¶xj )
- ¶¦/¶t
=
åj=1k xj'( d/dt(¶¦/¶xj') - ¶¦/¶xj )
if ¶¦/¶t = 0
= 0
if d/dt(¶¦/¶xj') = ¶¦/¶xj j=1,2,..,k
which are the Euler-Lagrange equations.
d/dx ( åi=1k yi' ¶¦/¶yi' - ¦)
= åi=1k yi" ¶¦/¶yi'
+ åi=1k yi' d/dx ¶¦/¶yi'
- ¶¦/¶x
- åi=1k ¶¦/¶yiyi'
- åi=1k ¶¦/¶yi'yi"
=
åi=1k yi' d/dx ¶¦/¶yi'
- ¶¦/¶x
- åi=1k ¶¦/¶yiyi'
=
åi=1k yi'( d/dx(¶¦/¶yi') - ¶¦/¶yi )
- ¶¦/¶x
=
åi=1k yi'( d/dx(¶¦/¶yi') - ¶¦/¶yi )
if ¶¦/¶x = 0
= 0
if d/dx(¶¦/¶yi') = ¶¦/¶yi i=1,2,..,k
which are the Euler-Lagrange equations.
.]
Theoretical physics then becomes a quest for the One True Action Lagrangian density , usually assumed
real scalar and generating kinematic equations involving zeroth, first, and second differentials only.
Geometric (multivector-valued) Lagrangians extermised in the sense that each multivector coordinate is stationary under variation.
This is an intrinsically nonrelativistic approach in the case of multiple particulate systems since it requires
a favoured temporal parametrisation t with L(t,p,p') = L(p,p')
As "locally shortest routes", Geodesics are 1-extremals for the scalar path length
of ò0t ds|dp¿g(dp)|½ . Integrating a square root can be messy
but fortunately such paths also extremise
ò0t ds ds p'(s)¿gp(s))(p'(s))
where p'(s) denotes the (d/ds)p(s)
. _Be Thus we set
L(p,p',s) =
p'¿gp(p')|½ and
minimise scalar integral ò0t ds ds L(p(s),p'(s),s) by solving the N Euler-Lagrange equations
d/ds(¶L/¶pi') =
¶L/¶pi) for i=1,2,...N .
L(p,p',s) will generally depend on p via _gp but if _gp has a symmetry such that
¶L/¶pi=0 for a particular coordinate i then
¶L/¶pi' is constant along any geodesic path.
Geodesic flow can consequently be viewed
as arising from a Lagrangian density
L(p(t),p'(t)) = |p'(t)¿_gp(p'(t))|½ .
with particles following timelike trajectories that extremise (minimally) their proper time (arclength).
If t is proper time parameterisation then
L(p(t),p'(t)) = |p'(t)2|½ = 1 along a geodesic.
Electrodynamical forces due to a 1-vector four-potential ap (typically with Ñp¿ap=0) are introduced by adding scalar
-q p'(t)¿ ap(t)
to the Lagrangian density leading to the Lorentz force law
mp"(t) = qfp.p'(t)
where fp = ÑpÙap .
[ Proof :
L = m(-p'2)½ - q p'¿ap
Þ ÑpL =
Ñp(m(-p'2)½ - q p'¿ ap)
= -qÑp(p'¿ap) ;
Ñp'L =
-m(-p'(t)2)-½ p'(t) - qap
so the Euler-Lagrange equation is
qp'¿Ñpap =
(d/dt)(m(-p'2)-½ p' + qap )
= mp" + q(p'¿Ñp)ap
Þ mp" = q(Ñp(ap¿p') - (p'¿Ñp)ap))
= q(ÑpÙap)¿p'
.]
Extremal surfaces
A more geometric generalistaion is to consider the problem of finding the M-curve of given content
maximising a particular boundary or interior integral. We might, for example, seek the loop
starting and ending at a given point a and constrained to lie in a given 2-curve (surface) containing a that maximises
enclosed content (area) for a given boundary content (pathlength)
Of fundamental importance is the fact that spacial Lagrangian density
(Ñ[e123]yp)2 is extremised for integration over CM
(subject to constraint of given boundary values over dCM) if yp
satisfies the spacial Laplace equation Ñp [e123]2yp = 0
over CM .
In electrodynamics we have L = - 2-4p-1 fp2
+ c-1jp¿ap
where c is scalar lightspeed and fp = ÑpÙap extremised by solutions to
Maxwell equations.
×××××××××××××××××××××××××××××××××××××××
 References/Source Material for Multivector Physics
References/Source Material for Multivector Physics
Anthony Lasenby
"Recent Applications of Conformal Geometric Algebra" 2005
http://www.mrao.cam.ac.uk/~clifford/publications
Leo Dorst. Daniel Fontijne, Steve Mann
"Geometric Algebra for Computer Science"
Morgan Kaufmann 2007
[Amazon US UK]
http://www.geometricalgebra.net
David Hestenes
"New Foundations For Classical Mechanics"
Kluwer Academic Publishers, 1999
Next : Multivector Relativity
Glossary
Contents
Author
Copyright (c) Ian C G Bell 2006, 2014
Web Source: www.iancgbell.clara.net/maths
Latest Edit: 15 Jun 2014.




