Those familiar with other treatments of relativistic mathematics, even the few multivector based ones, will find unorthodox notations here.
In particular, brackets are used in preference to precedence conventions (in accordance with programmer morality)
and "subscripts" emphasising positional (event) dependence are seldom ommitted.
Explicit S symbols ares used in preference to evoking a "summation convention"
for repeated ("dummy") indices.
We retain use of the
contractive inner product
( ¿ )
in preference to the conventional (Hestenes) inner product ( . ) where possible.
Since a¿b = a.b for 1-vector a whenever b has a zero scalar component,
the products are equivalent in many contexts.
Minkowski and Hestenes SpaceTimes
Minkowski SpaceTime Â3.1
Let (e1,e2,e3) be an orthonormal orientational reference frame for a Euclidean
3D space Â3. We
embody the concept of "time" by postulating a fourth vector e4 orthogonal to e1,e2,e3
with e42=-1 thus creating a basis (coordinate frame)
E=(e1,e2,e3,e4) for
Minkowski spacetime Â3,1 .
Note that e4 is sometimes given nonunit magnitude c
» 3 × 108 meter/second » 228 meter/second
(the "speed of light")
making a light year approx 1016m » 253m
but we retain "natural units" with c=1 here.
It is all too easy, encouraged by the name, to confuse lightspeed with photon speed. Some photons travel
very slowly in some mediums, and reference to a speed "in vacuum" requires an unrealistic
notion of vacuum uncluttered by "quantum foam".
When thinking about lightspeed one should forget about photons and consider c as the e4-independant
e4-observed instantaneous speed of a null trajectory. Physicists think of "massless particles"
in the sense of null four-momentum but this too
is misguided for we must ultimately associate mass with accelaration rather than momentum, and "lightspeed" trajectory need not be straight.
The current human estimate of c was obtained by measuring the speed of photons through nonvacuum, and became "exact"
by redefining the meter in terms of that estimate. Consequently, to the extent that humans underestimate the geodesic lightspeed, the "meter" is longer than our meter rulers.
We can extend E
to a basis for Â3,1 ( spacetime multivectors).
i=e1e2e3e4 , the unit pseudoscalar spanning spacetime,
(anti)commutes with all (odd)even multivectors and satisfies i2 = -1 ;
i§ = i .
Â3,1 <0;4>-multivectors a + bi having only scalar and pseudoscalar parts
form a subalgebra under the geometric product isomorphic to "complex numbers" Â1,1+
and commute with all even multivectors ( Â3,1+ ).
Note that
(a + bi)(a + bi)§ =
(a + bi)2 = a2-b2 + 2abi .
We say a spacetime 1-vector v is spacelike if
v2 > 0 , timelike if v2 < 0, and null (aka lightlike)
if v2 = 0.
We say a 1-vector is forward if v¿e40 < 0 for some universally agreed timelike e40.
Null vectors other than 0 are called proper null.
Let spacelike V satisfy V¿e4 = 0 (so that V Î e4*).
If V2 < 1 then e4+v is forward timelike (so not null) and we can define another forward timelike unit vector
f4 = (e4+v)~ = gV(e4+v)
where positive scalar relativity factor
gV º (1-V2)-½
is 1 for V=0 increasing to ¥ for V2=1.
We also have
e4¿f4 = -gV ;
(e4Ùf4)2 = gV2 - 1
; and
v = -^(f4,e4) / (f4¿e4) = (f4Ùe4)e4 /(f4¿e4) .
If we apply the rotational rotor
Re4®f4 = f4(e4+f4)~
to {e1,e2,e3,e4} we obtain a new
orthonormal basis F = {f1,f2,f3,f4} for spacetime which is no less "fundamental"
than {e1,e2,e3,e4}.
We use e4 rather than e0 for the timelike extendor of Â3 as
a matter of subjective notational preference. It is mathematically irrelevant but computationally prudent
as wish to "retain" e0 for use in a higher dimensional embedding.
Minkowski TimeSpace Â1.3
Many authors, notably Hestenes, consider three basis vectors
g1,g2,g3
of negative signature and
one, g0 of positive signature and so work in
Minkowski timespace algebra
( aka. Hestenes spacetime algebra or S.T.A. )
Â1,3 rather than Â3,1. Their meanings
of the terms "spacelike" and "timelike" are consequently the reverse of ours here
with regard to signature signs.
As for Minkowski spacetime algebra Â3,1 , the pseudoscalar
i=g0g1g2g3
(anti)commutes with (odd) even multivectors and has i 2=-1 .
The phrase "Minkowski signature"
is frequently used for both {+,+,+,-} and {+,-,-,-} but these two approaches (aka. the east coast and west coast metric )
, while substantively similar in some
regards, are not equivalent.
Null <1;4>-vectors
have 1-vector components of positive square in both alegebras, so have
"timelike" 1-vector component in Â1,3 but "spacelike"
1-vector component in Â3,1.
This author favours that spatial "squared distance"
be considered as "positive", temporal "squared distance" as "negative" since this
segues better with standard non-relativistic models - and we will
accordingly work with Minkowski spacetime algebra Â3,1 here.
Our "timelike" e4 thus has e4-1 = e4 = -e4 whereas
g0-1 = g0
= g0 .
Nullvector Decomposition
Given an arbitary nonzero 1-vector s with s2=0 then for any unit minussquare e- we can express s as
-(s¿e-)e- + (s+(s¿e-)e-) as the sum of orthogonal 1-vectors each of square
± (s¿e-)2 . Assume that l = (s¿e-) <0 , ie. that s is "forward" with regard to e- .
Taking e-' = (e- + ds)(1-2dl)-½ for any
d > ½l-1
we obtain
l' = s¿e-' =
l (1-2dl)-½ which can be made arbitarily small
for large d (taking e-' "closer" to s) or arbitarily large (negative) by taking d close to
½l-1 .
Thus means we can rechoose e- to ensure l<-1 and having done so, setting
postive d=½l-1(1-l2) yields s¿e-' = -1 .
Thus we can express any non zero forward nullvector as the sum of a unit forward minussquare vector and an orthogonal
unit plussquare vector.
This is profoundly important from a physical perspective since it implies null vectors cannot be meaningfully thought of as scaled.
We might think that the nullvector l(e-+e+) for l>1 is somehow "bigger" than e-+e+
but as we can find unit othonormal e-' and e+' such that l(e-+e+) = e-'+e+' , in what sense it bigger
"in kind"?
We can only speak of scale of nullvectors with referenece to another favoured (timelike, spacelike or null)
direction d not parallel to s, since d¿(l(e-+e+))= ld¿(e-+e+) then provides a d-dependant scalar measure of the "length" of s.
Note that the decomposition into orthonormal components is not unique, for by our construction above e-' lies in the 2-plane spanned by
sÙe- . If however we are given a nullvcetor s and an associated nonparallel 1-vector a this induces a unique decomposition of s
into e-+e+ where e- and e+ are orthornormal 1-vectors in sÙa.
Alternative spacetime representations
We can represent Â1,3 1-vectors
in Â3 as x = x1e1 + x2e2 + x3e3 + x4
provided we use x»¿x as our inner product
where » is a conjugation negating 1-blades but preserving scalars known in this context as space reversal
or conjugation. Clifford conjugation §# negating only odd-grade blades is suitable.
A disadvantage of this approach is that it is that differing observers
disagree on the grades of blades. By incorporating a fourth 1-vector of opposite signature to the spacial
ones, we can "make geometry invarient" and keep conjugations such as § and D observer-independant.
Points as Events
We refer to points in spacetime as events. If we wish to specify a particular event
as being a spacetime location where something does (or did) "happen" we will capitalise as Event.
Note that a basis (N-frame) E provides only an orientation of spacetime.
It does not embody any form of "origin" or "base event".
We say an event p is "percieved" by "observer" E at 0 to have occured at "place"
^e4(p) at "time" ¯e4(p). That is, we decompose p as p=P+te4 where pÎe4* is perpendicuular to e4.
[ Note that a realworld observer typically "becomes aware of", or
registers, an event
significantly after its "perceived" occurance due to finite signal speeds.
We attribute our observers with sufficient knowledge and computational acumen to calculate for
such delays and by "perceive" we really mean
"retrospectively deduces to have occured".
The theory of special relativity, now supported by significant experimental evidence, follows directly from the Minkowski model, without need of any reference to "light".

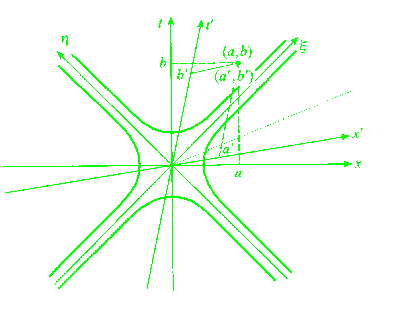
| A 2D Minkowski Diagram (from Rindler). The dotted line represents the putative worldine of supralight (v2>1) traveller. The indicated event is perceieved as (a,b) by observer E with frame (x,t) but as (a',b') by an observer E' with frame (x',t'). Hyperbolae denoted h and xi represent events "unit seperated" (p2=±1) from the common "origin" event agreed by E and E'. |
A worldine form of particular interest is
p(t) = (½tb)↑p(0)(-½tb)↑
with p'(t) = b×p(t) , where
b is constant (independant of t).
Picturing Minkowski Geometry
Planes and Simplexes
The first thing to note is that k-planes are still "flat". The solution set to
a1x1
+a2x2
+a3x3
-a4x4
= d
in Minkowski spacetime
looks a lot like the solution space to
a1x1
+a2x2
+a3x3
+(-a4)x4
= d
in a Euclidean space.
Thus k-planes are still essentially slices of slices.
To imagine, say, a 2-simplex (a0,a1,a2} _in Minkowski spacetime first ask what a 2-simplex is
geometrically. It is the convex hull containing 3 points, ie. a flat trianglar "facet" "hanging" in spacetime. The extended simplex is the 2-plane containing the triangle.
Let us first assume ((a1-a0)Ù(a2-a0))2<0 corresepnding to spacially seperated a0,a1 amd a2.
We can then postulate an observer
Stationary Stan travelling at e4 normal to this 2-plane so that Stan percieves all three events
as simultanous. Stan sees a triangle appear instantanously and then vanish immediately. Imagine this
momentary triangle and colour the edges red and the interior area green. Put white dots at each vertex.
Because this triangle exists in a 2D subpace of 3D space we can forget about "height" and imagine
a stack of 2D timeslices only one of which is non empty. Imagine slowly sweeping a 3D 2-plane representing the
perception of another observer Olly whose worldline is only slightly deviated from e4. Olly sees a white dot appear (event a0 say) which immediately diverges into
two red dots connected by a green line. These red dots drift apart
, the green line lengthening
, till suddenly one of dots flashes white and revereses its direction (event a1 say) and drifts back to rejoin
the other red dot at event a2. Both dots vanishing in a white flash. It is important to recognise that
Olly sees these red dots as moving "faster than light".
We colour timelike edges pink rather than red and so imagine a spacial 2-simplex as appearing to any observers as an instantaneous white flash, a pink dot travelling
at sublight speed for a while before vanishing in a white flash. Particular observers see the pink dot as stationary.
Simultaneity and Chronological ordering
In the above, Olly also sees events a0,a1, and a2 as spacially seperated,
but as non-simultaneous. He considers a0 to occur "before" a1 and both to occur "before" a2. Another observer Pete
with a different velocity to both Stan and Olly might also see a0,a1 and a2 as non-simultaneou, but disagree on their choronolical ordering.
Perhaps percieving a1 as the "initial white flash", a2 as the "bounce", and a0 as the "merge and vanish" .
Observers differ on the chronological ordering of spacelike seperated events, but agree
on the chronological ordering of timelike seperated events.
Impossibility of FTL Signalling
The essential problem here is that any given spacelike vector is regarded as temporally "forward" by some observers and "backward" by others.
Consider two spacelike sperated events 0 and ve1 + e4 with
scalar v > d > 1. As percieved by E, it would require a speed v
for an object to pass through both events on a straight line trajectory.
Suppose an object does so, then explodes at ve1 + e4 as the result of a hidden bomb.
Now consider an origin-coincident observer F with f4 = (e4+d-1e1)~.
[ f4 is timelike since f42 = -1 +d-2 < 0 ]
F percieves the object as being intact at F-time 0 and the explosion as occuring at F-time
f4¿(ve1 + e4) < 0 prior to the time of intactness.
[ -(e4+d-1e1)~¿(e4+ve1)
= (1 - vd-1)/|(e4-d-1e1)| < 0 ]
F does not have prior knowledge of the explosion at event 0, note. He cannot warn the object of it's doom
as they pass at _tE=_tF=0 . F only becomes aware of
the explosion having occurred when light from ve1 + e4 reaches him at a later positive F-time.
But what F deduces
to have occurred, figuring for the finite signal speeds, violates physical laws as he understands them;
a clock travelling with the object appears to F to run backwards. Thus anything capable of travelling faster than light
would have to be unchanging, or obey temporally reversible physical laws.
Suppose now that E sends sends a signal from 0 to ve1 + e4 recieved by origin-displaced
observer F having worldine
ve1 + e4 + t(e4+d-1e1)~ . Since F regards event 0 as happening at time
f4¿(-(ve1 + e4)) >0 then if F is also allowed to send an FTL "responce" signal he could potentially relay
E's signal to event 0-de4 for a small positive d, causing E to recieve the "responce" before sending the original.
This is known as a temporal loop.
One way to prohibit such loops is to disallow FTL signalling. Another is to impose
a favoured temporal direction on space (eg. radially outwards from an agreed centre)
and allow only "forward" FTL signalling with regard to this direction, so preventing looping back.
This has the interesting effect of making the average "outward" velocity far greater than the average "inward" velocity,
leading to an expanding universe in the sense that matter gets further from the agreed centre,
Spacetime Multivectors
Hyperbolic Spinor Representation of 1-vectors
Suppose 1-vector x = x1e1+x2e2+x3e3+x4e4 is forward timelike, ie. x2
= -|x|2 < 0 ; x4 > 0 .
Let X
º Xx,e4 º ^e4(x) =
x1e1+x2e2+x3e3
so X2 = |X|2 = ^e4(x)2 = (xÙe4)2 .
x~4 º e4¿x~ =
x4|x|-1 = x4((x4)2-(x1)2-(x2)2-(x3)2)-½ ³ 1
has (x~4)2 - 1 = |X|2|x|-2 .
For x2 £ 0,
ÑX|x|k = -kX|x|k-2
and in particular ÑXx2 = 2X
Pure plussquare scaled 2-blade x º xÙe4 = Xe4 is sometimes refered to as a relative vector.
It anticommutes with e4 .
We define the natural magnitude of x by kx º k º ln(|x|) = ¼ ln(x4) whenever x2¹0 .
We define the e4-dependant scalar hyperbolic parameter or rapidity of
a forward timelike 1-vector x by
c º cx,e4 º
cosh-1(x~4)
= ln(x~4 + (x~42-1)½)
= ln(x~4 + |X||x|-1)
= ln(x4 + |X|) - ln(|x|)
[ ln(a)ºloge(a) denotes the scalar natural logarithm function ]
so that
x4 = cosh(c)|x|
; |X| = |x| sinh(c) .
x = |x|(-cx~)↑ e4
= (k - cx~)↑ e4
= (|x|½(-½cx~)↑)§(e4)
= (½k -½cx~)↑§(e4)
is the e4 specific hyperbolic spinor form
representation of events inside forward null cone L+0 by
by positive scalar "length" |x|=(-x2)½, positive scalar rapidity c,
and a unit plussquare 2-blade
x~ º (xÙe4)~ = X~e4 = (Xe4)~ .
Ñxx~ = ÑxX~e4 = (N-2)|X|-1e4 where N=4 unless we add more spacial dimensions.
For spacelike x we have minusquare x~ and phase l º lx,e4 º cos-1(x~4) and trigonometric spinor form x = |x|(-lx~)↑ e4 .
For null x we have c=¥ and require either |X| or x4 to recover x from
x~ .
cx4e4,e4=0 and cx®¥ as x2®0.
c is a fundamental parameter for x because timelike 1-vector
Ñxc = |x|-2(x4X~ + |X|e4)
= |x|-1(-cx~)↑ X~
= |x|-2xx~
= |x|-2x¿x~
is normal to x ,
with x(Ñxc) = x~ .
Furthermore
Ñx2c = (Ñxc)2 = |x|-2 is independant of our choice of e4.
ÑXc = |x|-2x4X~
has (ÑXc)2 = ÑX2c = |x|-4(x4)2 .
[ Proof :
¶ cosh-1(a)/¶a = (a2-1)-½ and
Ðe4x~4
= |x|-1(1-|x|-2(x4)2)
= -|X|2|x|-3 so
Ðeic = (x~42-1)-½Ðeix~4
= (|X|2|x|-2)-½x4Ðei|x|-1
= (|X|-1|x|) x4xi|x|-3
= |X|-1 |x|-2 x4xi
for i=1,2,3
Ðe4c = (x~42-1)-½Ðe4x~4
= -(X2x-2)-½|X|2|x|-3
= -|X| |x|-2 .
Ñxc = åi=13 ei|X|-1 |x|-2 x4xi - e4|X||x|-2
= |x|-2(|X|-1 x4X + |X|e4)
= |x|-1( cosh(c)X~ + sinh(c)e4)
= |x|-1( - cosh(c)x~ + sinh(c))e4
= |x|-1( - cosh(c) + sinh(c)x~)x~e4
= |x|-1(-cx~)↑ X~
x(Ñxc)
= |x| (-cx~)↑ e4 |x|-1(-cx~)↑ X~
= e4X~ = x~
Ñx2c
= åi=13 (|X|-1 |x|-2 x4xi)2 - (|X||x|-2)2
= (|x|-2x4)2 - (|X||x|-2)2
= (|x|-2)2(x42 - |X|2)
= |x|-2
.]
The e4-speed of a 1-vector x is (e4¿x)-1 ^e4(x)2 . It is xero
for x=±e4, and 1 for null x, it is independant of the scale of x. It is 1 for null x and less than 1 for x2<0.
Canonical Rotor Form of Even Spacetime Multivectors
Before discussing the physical implications of Minkowski spacetime we will make an important
mathematical observation. The even subalgebra Â3,1 + is equivalent (isomorphic) to Â3 since the former is generated by
orthornormal anticommuting bivector "basis" {e14,e24,e34} with
e142=e242=e342=1 .
Any nonnull even R3,1 multivector b can be uniquely expressed as
b = R(reib)½ = (reib)½R
where
(reib)½ º r½( cos(b/2)+i sin(b/2))
for scalar r, b
and R=b(bb§)-½ is a unit rotor (ie. an even multivector
satisfying R§=R-1).
[ Proof :
(bb§)§ = bb§ Þ (bb§)<2>=0 .
For even bÎ R3,1 , bb§
= b<0>2 + b<4>2 - b<2>2
which remains even so the absence of a bivector component allows
bb§ = rea+ib
Þ (bb§)-½ = r-½e-½(a+ib)
which commutes with all even
multivectors and so with R
.]
This is known as the canonical form or invariant decomposition
of b .
Since i§=i and i (anti)commutes with (odd)even multivectors we have
b§(a) º bab§
= reibR§(a<+>)
+ rR§(a<->)
" a .
For nonnull pure bivector b2 we have b2b2§ = -b22 so that
b2 =c2eif
with timelike bivector c2 = r½R and scalar f=½b.
A null bivector b2 can be expressed as b2 = sceif
where s is a null 1-vector and c a unit spacelike (c2=1) 1-vector orthogonal to s .
Canonical Exponentiated Form of Even Spacetime Mutivectors
In Â3,1 we have three distinct forms of 1-spinor:
eqa =
cosq + a sinq if a2 = -1 ;
coshq + a sinhq if a2 = 1 ;
and 1+a if a2 = 0.
Most Â3,1 rotors can be expressed as
R=e½a2 for nonnull (possibly nonunit) bivector a2, the remainder require
R=±e½a2
=±(1+½a2)
with a22=0.
For a22 ¹ 0 we have a2=l(ae1234)↑c2 = l( cos(a)c2 + sin(a)e1234c2)
where l=|a2|, decomposing a2 into commuting plussquare and minussquare 2-blades.
for scalar a and unitsquare 2-blade
c2 .
Most Â3,1+ multivectors can thus be expressed
in spinor-factored or canonical exponentiated form
as
b= (r(ib)↑)½R
= r½(½bi)↑(½l(ia)↑c2)↑
= (½(r↓ + bi + l cos(a)c2 + l sin(a)ic2))↑
for 2-vector c2 with c22=1 and positive scalars r,l,a.
= (½(r↓ + bi + qc2 + fic2))↑
where
q = l cos(a) and f = l sin(a) .
Spinor (½l cos(a)c2)↑ is known as the boost factor of the rotor
since its effect taking c2=e34 is an accelartion in the e3 direction.
[ we can safely "combine" the exponentiations since all terms commute, c2 being even.
]
We then have
b↓ = ½(r↓ + bi + l cos(a)c2 + l sin(a)ic2)
A "degenerate" subclass of Â3,1+ multivectors
has the form
b = a(½bi)↑(1+a2) = (a↓+½bi+a2)↑
for null 2-vector a2 and two scalars a,b
and satisfies
bk = ake½kbi(1+2ka2)
;
b-k =
a-ke-½kbi(1-2ka2)
for integer k³0 .
Â4.2 Genralised Homegenised Minkowski Spacetime
We can extend Â3,1 by orthogonal null vectors e0,e¥ in like manner to
the Generalised Homegenised extension
ÂN% Ì ÂN,1
of Li et al and the arguments and proofs in our discussion of the Generalised Homeogenised Euclidean Space
carry into the Minkowski case Â3,1% Ì Â4,2 without difficulty to give
Generalished Homogenised Minskowski Spacetime or GHMST aka.
conformally extended spacetime.
Most generally, we extend N-D space UN with basis { e1,...,eN }
by two orthogonal vectors e+ and e- satisfying
e+2 = 1;
e-2 = -1;
e+¿e- = 0
to form an (N+2)-D space UN% with basis
{ e0,e¥,e1,...,eN } where
e0 = ½(e- - e+) ;
e¥ = e- + e+
are null vectors. We have bivector
e¥0 º e¥Ùe0 = e+Ùe- =
e+e- with properties e¥02=1 ;
e¥0§ = e¥0§# = -e¥0 ;
and "absorbtion" by the nullvectors:
e¥0e¥ = -e¥e¥0 = -e¥ ;
e¥0e0 = -e0e¥0 = e0 .
We define e0 º -e¥ ; e¥ º -e0. These satisfy
e0¿ e0 = e¥¿e¥=1 but also e0Ùe0 = - e¥0 ; e¥Ùe¥ = e¥0
so serve only as "quasi-inverses" for e0 and e¥.
If i=e1Ù...ÙeN is a unit pseudoscalar for UN
then e¥0i is a unit pseudoscalar for UN%.
We can express any 1-vector x Î UN% as
x + ae0 + be¥ where x Î UN.
Our embeding is once again
x = ¦(x) = x + e0 + ½x2e¥
with inverse mapping
x = (e0¿x)-1 ^e¥0(x) =
(e¥¿x)-1 (e¥0Ùx)e¥0 when (e¥¿x)¹ 0 ;
and x=^e¥0(x) when (e¥¿x)= 0 .
This time, for UN=Â3,1, we are mapping into three distinct geometric spaces.
Spacelike x map to the e¥¿x>0 half of the horosphere ;
timelike x map to the e¥¿x<0 half of the horosphere ; while
null x map to L0 + e0 as x ® x+e0.
In particular, e0 corresponds to an arbitary UN origin 0, while
e¥ represents a hypothetical UN point at infinity ¥.
If a,b are the null UN% 1-vectors associated with UN points (events) a and b, we have:
a¿b =a.b = -½(a-b)2
= -½(a-b)2 ;
aÙb = aÙb +½(a2b-b2a)e¥
+ (a-b)e0 - ½(a2-b2)e¥0.
As for ÂN%, if a0,a1,...ak are k+1 1-vector points (events) in UN then
e¥Ùa0Ùa1Ù...Ùak
= e¥Ù(a0 + e0)Ùak
represents the UN extended simplex {a0,a1,...ak}.
For k=3 the simplex extends into the 3-plane through a0 with tangent a3 = (a1-a0)Ù(a2-a0)Ù(a3-a0) .
In Â3,1, if a32<0 with then the dual
a3* is a timelike 1-vector representing the wordline direction of an observer percieving
all four events as cotemporaneous. The simplex itself is percieved by this observer as a convex hull of 4 cotemporaneous points, ie. an instantanoues tetrahedral volume.
Further,
(e¥Ùa0Ùa1Ù...Ùak)2
=... = ((a1-a0)Ù...Ù(ak-a0))2 giving the square of k! times the content of the simplex.
As for ÂN%, a UN% (k+1)-blade ak = a0Ùa1Ù...Ùak derived from events a0,a1,..,ak has geometrical interpretations:
We attach no physical significance to the e+ and e- dimensions, considering them as wholly abstract constructs
facilitating the computation of intersections.
Â5.2 Spacially Extended GHMST
For reasons which will become clear later, we will extend Minkowski space time by a fourth spacal dimension
to which we will regard as physically significant rather than a mere computational aid. We thus regard the physical universe as being modelled by
a structure in Â4,1 and we add general homogenising dimensions e0 and e¥ as before
to represent k-spheres and k-planes in Â4,1 as (k+2)-blades in Â5,2.
We will denote the fourth spacial dimension with e5, retaining e4 for the timelike axis, rather than
taking e4 spacelike and e5 timelike.
The Â4,1 unit pseudoscalar e12345 commutes with everything in Â4,1, squares to -1, and reverses to itself.
The Â5,2 unit pseudoscalar e¥0e12345 commutes with everything in
Â5,2, squares to -1, and is negated by reversion.
Since any multivector in Â4,1 can be expressed as a+be12345=c+de1234 for a,b in Â4 and c,d in Â3,1 we have Â4,1 isomorphically equivalent to both C4 and C3,1 with e12345 taking the role of central complex scalar i. Note that such a "dimension reducing complexifications" are e4- or e5-dependant.
It is worth explicitly noting that Â4,1 "contains" Â1,3 as the subgroup generated by the four anticommuting 4-blades { e1*,e2*,e3*,e4* } where ei* = eie12345-1 .
For now we will ignore our "fifth dimension" and assume that all multivectors have zero
e5¿a=0 unless expliticly stated otherwise, ie. the coefficient of any blade including e5 is to be assumed zero.
k-spheres and Nullcones
Nullcones
We refer to L-c = { r : (r-c)2 = 0 & (r-c)¿e4 > 0 }
as the rear null cone (aka. rear lightcone) at c. If we extended UN into UN% using generalised hompgenised coordinate
extenders e0 and e¥ in the usual way, then L-c is represented by null (N-1)-blade
c* = (e0+c+½c2e¥)*
We refer to L-c· = { r : (r-c)2 £ 0 & (r-c)¿q > 0 }
as the filled rear nullcone at c with regard to an understood timelike direction q.
We refer to L-c,q,l· = { r : (r-c)2 = 0 & (r-c)¿q = l }
as the l-past at c for timelike direction q.
In a flat (homegeneous) Â3,1 space all rear nullcones are displacements of
the origin rear nullcone L-0.
Lp = (p+e0+½p2)* in Â3,1% embodies the nullcone at p
and in particular L0 = e0* = e0i-1 respresents the nullcone at 0 .
We can intersect with this nullblade by lifting into Euclidean space, but projection is problematic.
¯_wigwog(p) simply rescales p such that p2=d so
Limd ® 0 ¯ Od,c(p) = c.
Given a timelike unit d nonparallel with v=p-c we have v=ad + V
where a=-d¿v and V=v-ad is nonzero and orthogonal to d. We can then decompose
v = (a+|V|)(d+V~) - (aV~+ad) into orthogonal components and
define _prl3[p,c,d] = ¦(c + (a+|V|)(d+V~)) and
_Rflct2[ Lc,d](p) = ¦(c + |V|d + aV~) as d-directed projections and reflections in Lc.
Dirac D Function
The Dirac D function Âp,1 ® Â
is defined by
D(x) º 2d(x2) Sign(e4¿x) , ie. (somewhat informally) zero off the nullcone
L0 , +¥ on the forward nullcone L+0, -¥ on the rear null cone L-0 and zero at 0.
Though we have defined it with reference to a particular e4, D(x) is frame-independant in the sense that any
other "forward" e4' with e4¿e4'< 0 generates the same D(x).
Sign(x) = x|x|-1 is defined to be 1 for x>0, -1 for x<0, and 0 for x=0.
d(x) is the scalar Dirac delta function which can be loosely defined
as d(x) = _epslon-1(1-e-1|x|) for |x|£e and 0 for |x|³e
for very small e.
D(x) = |X|-1( d(x4-|X|) - d(x4+|X|) )
[ Proof :
ò-¥¥ dx¦(x)d(x2-a2)
=
ò-¥0 dx¦(x)d(x2-a2)
+ ò0¥ dx¦(x)d(x2-a2)
= ò¥-a2 dy¦(-(y2+a2)½)½(-(y2+a2)½)-1d(y)
+ ò-a2¥ dy¦((y2+a2)½)½((y2+a2)½)-1d(y)
= ½(¦(-a)a-1
+ ¦(a)a-1) = ½a-1(¦(a)+¦(-a) .
Hence since ¦ is arbitary we have
d(x2-a2) = ½a-1(d(x-a) + d(x+a)) .
Whence d(x2) = d(-x2) =
½|X|-1(d(x4-|X|) + d(x4+|X|)) and the result follows.
.]
It can be shown [ Dirac 75.23 ] that for p=3 we have
ò d4x D(x) (i k¿x)↑
= 4p2i D(k)
with geometric form
ò d4x D(x) (b k¿x)↑
= 4p2 D(k) ib for any b with b2=-1.
Since k2 D(k)=0 we obtain
Ñx D(x) = 0.
Tspheres and Tballs
We will here refer to the instersection of a "filled" hypersphere or "ball" { p : (p-p0)2 £ r2} in a Minkowski space with a nonspacial k-plane (ie. a k-plane containing a timelike 1-vector) as a k-tball. We will refer the the boundary of a k-tball (the "surface" of the k-sphere) over which (p-p0)2 = r2 as a k-tsphere . We will reserve the terms k-sphere amd k-ball for structures in Euclidean (sub)spaces.
A (N-1)-tsphere or hypertsphere in ÂN,1 with centre event c and
positive radius r is a hypercurve, the set of all events satisfying
(p-c)2= r2.
All observers percieve it in the same way. Simultaneous with event c they percieve a spacial 2-sphere
(ie a 3D "globe") of radius
r centre c and surface area 4pr2 and volume (4/3)pr3 which then increases in radius at an ever increasing sublightspeed. At time ±t,
they percieve a (spacial) 2-sphere of radius (r2+t2)½
centre c±te4 . A 3-tsphere centre c is thus percieved by all observers as
a 2-sphere of infinite radius at time t=-¥ that contracts to radius r at time t=0 and then expands again
as t increases, always centred at ¯e4*(c) where e4 is observer specific. The content of a
tsphere is infinite.
A k-tsphere of radius R is the intersection of a hypertsphere (p-c)2=R2
with a nonspacial (k+1)-plane
. For any r³R we
can find a hypertsphere of that radius which will serve but it is natural to specify r=R so that
the k-tsphere is a "maximal slice" of the hypertsphere. We thus regard a k-tsphere of radius R centre c as the
intersection of a hypertsphere of radius R centre c and a (k+1)-plane through c.
An observer with timelike e4 normal to the plane will observe an instantaneous spacial (k-1)-sphere contemporaneous with centre event c.
An observer with spacelike e3 normal to the plane will observe a phenomena constrained spacially to plane e124
through c.
The intersection of a k-tsphere with a spacial (l+1)-plane (ie. a (l+1)-plane
whose tangent (l+1)-blade spans no timelike 1-vectors) for m<l is a l-sphere.
A 3-tsphere of negative radius -r<0 and centre c is the set { p : (p-c)2=-r2 } .
This has two components or pieces and divides spacetime into three regions, wherwas positive r hypertsphere have one component and divide spacetime into two regions.
O+-r,c is seen by all nonaccelerating observers as a sphere
of radius ¥ at t=-¥ that contracts at increasing supralightspeed to radius 0 at
t=-r before event c whereupon nothing exists until
t=+r after c when a spacial 2-sphere of zero radius appears, expanding at decreasing supralightspeed to infinite radius at t=¥.
At t=r0±d the radius is (2r0d+d2)½.
We can regard O+-r,c as the set of all points reachable by a straight-line travelling particle
starting from event c with any timelike unit velocity v after time r as measured by the particle.
Although O+-r,c approaches the nullcone L+c for large e4¿(p-c) its content is infinite.
We have a more general form of the Dirac Delta function
Dr,c(x)
º 2d((x-c)2 + r2) Sign(e4¿(x-c))
= = (X2+r2)-½(
d(x4-(X2+r2)½)
- d(x4+(X2+r2)½ )
which is zero off O+-r,c and ±¥ in the forward/backward components of the hypertsphere.
Extending to Â4,1 with x5=_cu5=0 we have
Dr,c(x) = D(x-c-re5) .
The 3-tsphere of zero radius and centre c is of course the nullcone at c so O0,c = Lc . A k-tsphere of zero radius, centre c is the projection of Lc into a k-plane through c.
1-tsphere
A 1-sphere is a ring in spacetime with timelike axis n. There are observers who percieves an instantaneous red hoop but most see two red particles (no white flash) which appear together but fly apart following two symmetic trajectories at FTL speeds to recombine slightly more than 2S from their appearance point a moment later. S
A 1-tsphere of postive radius is a timelike 1-curve
p(t) =
S(S-1te43)↑e3
= S(½S-1te43)↑§(e3)
= S( cosh(S-1t)e3 + sinh(S-1t)e4) .
p(t)2 = S2 ; p'(t)2=-1
which is the natural parameterisation of a
timelike path of a particle maintaining a constant
seperation S from a particular event 0. It is e4-percieved as a trajectory coming from
¥e3 at time t=-¥ having nearlight velocity towards O ,
subject to a uniform repulsive bivector forcefield
Wp = Wp = p"(t)p'(t) = S-1e34 and passing
spacially closest to O at Se3 at t=0 before moving back off towards ¥e3 again, approaching the lightcone L+0
as it constantly accelerates towards lightspeed.
The future hemitspherical half of a 1-tsphere of negative radius
is the naturally paremeterised spacelike path
p(c) = S(S-1ce43)↑e4
= S(½S-1ce43)↑§(e4)
= S( cosh(S-1c)e4 + sinh(S-1c)e3)
has p(c)2 = -S2
;
p'(c) = (S-1ce43)↑e3
;
p'(c)2 = 1 and can be viewed either as the path of a FTL particle maintaining a constant
seperation S from event 0 (passing through event Se4 at c=0)
or (for -¥ < c < ¥ ) as the loci of all possible points
reachable by a particle travelling in a straight timelike trajectory from event 0 after time S
as measured by the particle.
A (N-1)-tball or hypertball of centre c and radius S is the set
{ p : (p-c)4 <S4 } . It is accordingly a "solid" rather than a "surface"
and acts like a "thick null cone" for small S. It contains the frame-dependant "hermitian sphere"
p†p = |p|+2 < R2 where † is Hermitian conjugation
associated with any given frame and so can be thought of as a "small event" .
Imposing a time frame e4, at time t a hyperball is percieved as { pÎÂ3 :
(p2 - t2)2 £ S4 } . For t>S this is a 2-spherical shell of inner radius
(t2-S2)½ and outter radius (t2+S2)½ and consequent thickness
t((S/t)2 + 24(S/t)6 + O((S/t)10))
= t-1S2 + O(t-5S6).
The content of this shell is approximately 4pt2 t-1S2
= 4ptS2 .
Next : Helices